数学の部屋
目次
| 失敗から学ぶ1 | カオス理論 |
| コラッツの問題 | ABC予想 |
| 幾何学再入門 | 正四面体の重心と頂点のなす角度 |
| ベクトル解析入門 | 部分積分と置換積分 |
| ベイズ統計にチャレンジ |
失敗から学ぶ1
失敗から学ぶ
｛参考：マシュー・サイド. 失敗の科学 失敗から学習する組織、学習できない組織｝
ハンガリー生まれの天才数学者ウォルド。ナチスの迫害を逃れて米国に渡る。実は家族9人のうち8人はナチスに殺されたとか。アメリカ渡った彼に軍からの依頼である重要な問題解決を頼まれた。
第二次大戦当時、 爆撃機のパイロットは極めてハイリスクな任務だったという。従軍中に生き残る確率は五分五分、50%ということ。「既死兵（ ghosts already）」と呼んだ人も。
軍司令部は爆撃機を強化するために装甲が必要と考えた。地上空中両方の敵の砲撃からパイロットを守るため。ただし、爆撃機全体を装甲で覆うと、機体が重くなりすぎて操縦が困難になる。空飛ぶ亀では役に立たないか。
ウォルドの任務は、装甲が必要な部分の優先順位を調査することだった。 データは沢山あった。空軍はすでに手間をかけて、無事に帰還した爆撃機の損傷具合を調べていたのだ。 彼等は失敗から得たデータを検証して、航空機の安全を高める方法を考えようとしていた。
辛くも帰還した爆撃機の損傷には明確なパターンが存在した。爆撃機の多くは、翼も胴体 も蜂の巣のように穴がたくさん開いていた。しかしコックピットと尾翼には砲撃を受けた 形跡がない。データの収集続ければ続けるほど、パターンはますます明瞭に。
これを知り軍令部は完璧と思われるアイデアを思いつく。「そうだ。沢山穴の開いていた機体部分にしっかりと装甲を施そう。砲撃を沢山受けた個所が強化すべきところだ。」
しかし、ウォルドは猛反対。読者の皆さんもお判りでしょう。
軍司令部は大事なデータを考慮し忘れている。軍は生還した爆撃機のデータしか集めていない。帰還できなかった（ 撃ち落とさ れ た）爆撃機は入っていない。帰還した爆撃機のコックピットと尾翼に穴の跡がなかったのは、そこを撃たれたら帰還できなかったからだよね。
言い換えれば、爆撃機の穴の跡は、そこなら撃たれても耐えられる場所を示しているんだ。言われてみれば馬鹿でも分かることだった。
検証データは、装甲が必要な場所では なく、不要な場所を教えていた訳だ。コックピット と尾翼を撃たれなければ、 パイロットは無事生還できる。
ウォルドの洞察は、軍事活動全体にとっても貴重な転機をもたらしたという。
この一件は、大事なことをいくつ か 教えてくれる。まず、失敗から学ぶためには、目の前に見えていないデータも含めて、すべてのデータを漏れなく考慮しなければいけない。
失敗から学ぶことは、そんなに簡単な訳ではない。そんな時はこのケースのように、注意深く考える力と、物事の奥底にある真実を見抜いてやろうという意志が不可欠だ。
この教訓は、数学の統計学の話とも言える。統計でデータ処理や数値解析を行う際、まず最初に行うべきことはデータの母集団の性質の把握だ。ここを怠れば、出て来た成果は全く使い物にならない虚偽のものになってしまう。
この例では、集められたデータは総て生還した機体のものだけだ。これをいくら分析しても無意味だね。欲しいデータは撃ち落された爆撃機も含む出撃した爆撃機全体のデータだ。しかも対策の目的は撃ち落されないように機体を強化するのだから。しかし、撃ち落された爆撃機のデータは多分収拾不能だろう。このように説明を受ければ当たり前のことに思えるけど、実際に自分が全く別の状況で同じ問題に遭遇したら適切に対処できるだろうか。
この事実は、現在流行中のcovit-19ウィルスについても考えられる。重症化して助かった人は、皆抗体を持っていた。だから抗体をつくるワクチンを注射すれば重症化は防げる。
でも、軽症の人や無自覚無症状で回復した人(PCR検査で陰性化した人)、ほとんど抗体が出来ていない。つまり、抗体は感染拡大を防ぐ効果はない。感染した結果生じるものらしい。
でも、HIVウィルスの検査では抗体所有者を感染者と断定している。
風邪と同じで多くのウィルス感染症は、抗体とは別の免疫機構(自然免疫と呼ばれている)で防御されている。感染の拡大を防ぐと言う意味からは、抗体ワクチン(mRNAワクチンも含む)は、無用の長物のようだ。或いは抗体検査そのものも。
scienceの部屋
カオス理論
カオス理論（chaos theory、中: 混沌理论、露: Теория хаоса）
とは、力学系の一部に見られる、数的誤差により予測できないとされている複雑な様子を示す現象を扱う理論である。カオス力学ともいう。
ここで言う予測できないとは、決してランダムということではない。その振る舞いは決定論的法則に従うものの、積分法による解が得られないため、その未来（および過去）の振る舞いを知るには数値解析を用いざるを得ない。しかし、初期値鋭敏性ゆえに、ある時点における無限の精度の情報が必要であるうえ、（コンピューターでは無限桁を扱えないため必然的に発生する）数値解析の過程での誤差によっても、得られる値と真の値とのずれが増幅される。そのため予測が事実上不可能という意味である。
カオスの定義と特性
ある初期状態が与えられればその後の全ての状態量の変化が決定される系を力学系と呼ぶ。特に、決定論に従う力学系を扱うことを強調して決定論的力学系とも呼ばれる。カオス理論において研究されるカオスと呼ばれる複雑で確率的なランダムにも見える振る舞いは、この決定論的力学系に従って生み出されるものである。この点を強調するためカオス理論が取り扱うカオスを決定論的カオス(deterministic chaos)とも呼ぶ。複雑で高次元の系ではなくとも、1次元離散方程式や3次元連続方程式のような非常に簡単な低次元の系からでも、確率的ランダムに相当する振る舞いが生起される点が決定論的カオスの特徴といえる。この用語は、カオス理論以前から存在するボルツマンにより導入された分子カオスと呼び分ける意味合いもある。ボルツマンによるカオスは確率論的乱雑さを表しており、カオス理論におけるカオスとは概念が異なる。
**つまり、サイコロを振るような確率的な現象でなく、一見完全に決定論的に決められそうな問題が、実はカオスであって予測不能だったりする。
カオス理論におけるカオスの厳密な定義は研究者ごとに違い、まだ統一的な定義は得られていない。できるだけ簡単な表現でまとめると、カオスの定義あるいはカオスと呼ばれるものの特性とは、「非線形な決定論的力学系から発生する、初期値鋭敏性を持つ、有界な非周期軌道」といえる。また、このような軌道を含む力学系の性質を指してカオスとも呼ぶ。軌道を指していることを明らかにする場合はカオス軌道(chaotic orbit)と呼ぶ場合もある。以下に、もう少し詳細に説明する。
非線形性
力学系には大きく分けて線形力学系と非線形力学系が存在するが、線形力学系ではカオスは発生しない。その系からカオスが生起されるためには、系が何らかの非線形性(nonlinearity)を持つ必要がある。言い換えると、軌道を生成する系が非線形力学系であることは、その系からカオスが生起されるための必要条件である。これの十分条件は満たされず、すなわち、非線形力学系であれば必ずカオスが生起するわけではない。以下に述べる特性と違い、非線形性はカオス軌道自体の特性というよりは、カオスを生起する系の特性といえよう。
初期値鋭敏性
カオスの定義あるいは特性として第一に挙げられるのが初期値鋭敏性(sensitivity to initial conditions)。これは、同じ系であっても初期状態に極僅かな差があれば、時間発展と共に指数関数的にその差が大きくなる性質。この性質は軌道不安定性(orbital instability)と言い換えられることもある。定量的には、この初期値鋭敏性は、リアプノフ指数、コルモゴロフ-シナイエントロピーなどで評価されるとされている。
初期値鋭敏性により極めて小さな差も指数関数的に増大していくので、初期値鋭敏性を有する実在の系の将来を数値実験で予測しようとしても、初期状態（入力値）の測定誤差を無くすことはできないので、長時間後の状態の予測は近似的にも不可能となる。このような性質は長期予測不能性(long-term unpredictability)や予測不可能性(unpredictablity)などとも呼ばれる。一方で、例えカオスであっても決定論的法則から発生されるものであるため、短時間内であれば有用な予測は可能といえる。以上のような性質は、標語的にバタフライ効果(butterfly effect)と呼ばれる。
有界性
初期値鋭敏性、すなわち指数関数的に初期状態の差が広がる軌道を有する系というだけでは、カオスには該当しない。カオス軌道であるためには軌道がある有界な範囲に収まる必要がある。このようなカオスの特性は有界性(boundedness)とも呼ばれる。
非周期性
カオスの特徴は、平衡点に収束するわけでもなく、周期的軌道に漸近するわけでもなく、非周期的な軌道を取る点。カオスが認識されるようになる以前は、非周期的な運動が発生するには、発生させる系自体も複雑なものだろうと考えられていたが、非常に簡単な決定論的な法則（力学系）からでも非周期運動が発生する点がカオスの特徴。平衡点収束と周期的軌道以外にも力学系では準周期的軌道と呼ばれる軌道も存在し、非常に複雑で不規則的な軌道を取るが、初期値鋭敏性を持たないことからカオスには分類されない。カオスが非周期軌道を取ることの特性は非周期性(nonperiodicity)などと呼ばれる。非周期的であるかどうかは、パワースペクトルが幅のある連続的スペクトルを示すかどうかなどで評価される。
以上は、Wikipediaの説明を基にしたものだが、実際には数学的な勉強をして見ないとなかなか理解できない。しかし、気象予報が短期的にはかなり正確に出来るのに長期予報は当たらない。経済予測は更に当たらない。これらは、予測担当者の能力の問題ではなく、気象現象自体がカオスの特徴があるためと考えた方が良いようだ。
長期予測不能性は、今欧米で危機感を以って政治的に叫ばれている気候変動問題にも当てはまるようだ。CO2濃度(0.03～0.04％)の変化がどのように気温変動に結びつくかは全く数学的に全く予測不能ということが科学的真理かも知れない。気温変動にはCO2濃度以上に大きな影響を与える要素が複雑に絡み合っている。
2022年、気候変動予測システムの開発で、眞鍋淑郎博士がノーベル賞を受賞した。眞鍋淑郎博士が開発したシステムは極めて複雑でスーパーコンピューターを使っても多大な時間を要するものらしい。ノーベル賞は開発の成功に対して与えられたものではなく、その蓄積された知識のノーハウに対して与えれたものらしい。
眞鍋システムで色々な条件で多数の実験を繰返せば、気候変動がカオスかどうかは調べられる。もし、気候変動がカオスなら、これは大きな科学的な成果で確かにノーベル賞に値する研究になる。
しかし、もし地球の気候変動がカオスとしての振る舞いをするならば、将来の気候変動を予測することは不可能であるとの結論になってしまう。脱炭素社会への取り組みがどれだけ意味のある行動になるのか。
つまり、今彼がノーベル賞を受賞したタイミングは、温暖化の仮定を既成事実化して、これ以上の研究を続けないようにするのが目的の政治的な判断だった可能性がある。眞鍋淑郎博士も言っている。「気候変動を予測することは極めて難しい。しかし、政治的な判断を下すことは更に難しい。」
scienceの部屋
コラッツの問題
コラッツの問題（Collatz problem）は、数論の未解決問題のひとつ。1937年にローター・コラッツが問題を提示。問題の結論の予想を指してコラッツの予想とも。初期にこの問題に取り組んだ研究者の名を冠して、角谷の問題、米田の予想、ウラムの予想、他にはSyracuse問題などとも呼ばれる。数学者ポール・エルデシュは「数学はまだこの種の問題に対する用意ができていない」と述べ、解決した人に500ドルを提供すると申し出た。 ジェフリー・ラガリアスは2010年に、コラッツの予想は「非常に難しい問題であり、現代の数学では完全に手が届かない」と述べた。
コンピュータを用いた計算により、268 までには反例がないことが確かめられた。 また、2011年度大学入試センター試験数学IIB第6問に題材として取り上げられた。
問題の概要
「任意の正の整数 n をとり、
n が偶数の場合、n を 2 で割る
n が奇数の場合、n に 3 をかけて 1 を足す
という操作を繰り返すと、どうなるか」
というもの。「どんな初期値から始めても、有限回の操作のうちに必ず 1 に到達する（そして 1→4→2→1 というループに入る）」という主張が、コラッツの予想である。
フリー百科事典『ウィキペディア（Wikipedia）』
問題の意味するところは、分かるだろう。電卓を使って、簡単な数で試してみれば、どうもそうなりそうだと想定できる。試した範囲では例外なく成立する。
最初の数は奇数から始めれば良い。偶数なら2で割るからどこかで奇数になる。
例えば、
13→13×3＋1＝40→20→10→5→5×3＋1＝16→8→4→2→1 →1 OK
7→7×3＋1＝22→11→11×3＋1＝34→17→17×3＋1＝52→26→13 OK(後は13と同じ)
25→25×3＋1＝76→38→19→19×3＋1＝58→29→29×3＋1＝88→44→22→11 OK(11も上にある)
9→9×3＋1＝28→14→7 OK(7も上にある)
101→101×3＋1＝304→152→76→38→19→19×3＋1＝58 OK(19も上にある)
因みに
1→1×3＋1＝4→2→1
どうも、この命題に反例は作れそうもない。でも、反例が存在しないことは証明できそうもない。つまり、この命題は未だに数学的に証明されていない未知の命題なのだ。一見すると高校で習った数学的帰納法で簡単に証明できそうなんですがね。
2021年10月26日の朝日朝刊でも取り上げられた。「コラッツ予想」証明出来たら1億2000万円の賞金。日本のベンチャー企業社長の福勢晋さんが解決に貢献したとのこと。
再度、問題を述べると、「どんな正の整数も、偶数ならば2で割り、奇数ならば3倍して1を足す。この操作を繰返せば、必ず最後には1になるだろう。」
数学には、どう見ても正しそう、つまり帰納法的な推論では納得できても証明されていない難問が多数存在している。そのうちいくつかは多額の懸賞金もかけられている。でも、証明に成功した人は皆高度な数学能力のある方ばかりだから、素人はのめり込まないのが無難かも。「四色問題は」コンピュータの力を借りて証明されたとされており、ではそもそも「証明とは何か」との議論まで起こされたとか。
scienceの部屋
ABC予想
ABC予想（abc conjecture）：
1985年にジョゼフ・オステルレとデイヴィッド・マッサーにより提起された数論の未解決予想。これは多項式に関するメーソン・ストーサーズの定理の整数における類似であり、互いに素でありかつ a + b = c を満たすような3つの自然数a, b, c の和と積の関係について述べている。
ABC予想は、この予想から数々の興味深い結果が得られることから有名になった。数論における数多の有名な予想や定理が ABC予想から直ちに導かれる。
**何ページにも及ぶ証明が数行で解決してしまうとも。だから重要なのでしょう。
Goldfeld (1996) は、ABC予想を「ディオファントス解析で最も重要な未解決問題」であるとしている。
**ディオファントス解析：ディオファントス方程式（Diophantine equation）とは、整係数多変数高次不定方程式である。文脈として、整数解や有理数解を問題にしたい場合に用いられる用語であり、主に数論の研究課題と考えられている。古代アレクサンドリアの数学者ディオファントスの著作『算術』で、その有理数解が研究されたのにちなんだ名称である。
証明の試み
ABC予想を証明するためのさまざまな試みがあるが、現在完全に数学コミュニティのコンセンサスが得られたものはない。
ところが、2012年8月30日、京都大学数理解析研究所教授の望月新一が ABC予想を証明したとする論文を京都大学数理解析研究所の編集する専門誌『Publications of the Research Institute for Mathematical Sciences』 (以下『PRIMS』)に投稿し、初稿が同誌のプレプリントで公開された。
(NHK; 2022年4月10日の放送内容から)
2020年4月。「ａｂｃ予想」と呼ばれる数学の重要な未解決問題を、日本人が証明したというニュースが駆けめぐりました。論文を書いたのは、京都大学数理解析研究所教授望月新一博士。世界的天才として知られてきた人物です。
ａｂｃ予想を証明した、博士の「宇宙際タイヒミューラー理論」。査読の完了と専門誌への掲載は、望月博士の偉業が、世界に正式に認められたことを意味しました。ところが…望月の証明はまだ受け入れられないと主張する数学者が多数現れ、今も激論が続いている。一つ一つ論理を積み上げていけば、誰もが同じ結論に達するはずの数学の世界。完全に正しいとする数学者がいる一方で、なぜ多くの数学者が理解できないというのか。ある数学者は言います。「その答えを知りたければ、ａｂｃ予想を解き明かしたという宇宙際タイヒミューラー理論が、これまでの数学と何が違うのか。それを理解しなければならない」と。これは、史上まれにみる異常事態に突入した数学界をめぐる数奇な物語です。→新しい数学の誕生ではないかと言う意見もある。
abc予想の証明を発表した望月新一博士は、わずか16歳でアメリカ･プリンストン大学に入学。23歳で博士号を取得した世界が認める天才です。一方で、社交的な場には、ほとんど姿を現さない、謎めいた人物としても知られています。ａｂｃ予想を解き明かしたという理論は、一体どんなものなのか。2017年、私たちは博士に取材を申し込みました。返ってきたのは一通の丁寧なメールでした。
「『宇宙際タイヒミューラー理論』が、今までの数学と何が違うのかといった問いかけは、一つの有意義なテーマであり、私自身も、多くの数学者と議論してまいりましたが、意味のある議論、もしくは解説が成立するには、非常に高度な専門知識が必要であり、一般の視聴者どころか、一般の数学者でもかなり厳しいものがあると言わざるを得ません。ご熱意に水を差すようで恐縮ですが、以上の理由によりお断りさせていただきます。望月新一」
プリンストン大学時代からの友人、ミンヒョン･キム博士は、望月博士が人前に姿を現さないのは、数学に対する集中力と忍耐力を保ち続けたいと考えているからだろうといいます。
フランス･パリ郊外に暮らす、ミッシェル･ワルドシュミット博士。ａｂｃ予想について教えてほしいという私たちに、「それならまず『かけ算は簡単だけど、たし算は難しい』ということを理解すべきだ」と語り始めました。
これ以上説明を聞いても所詮分からないでしょう。でも、この証明すべき命題(予想)が述べていることは決して分かりにくいものではないようです。
ABC予想
経緯：1985年 予想が提起→2012年望月論文発表→2020 査読論文
-------------------------------------------------------------------------------------
a＋b＝c を満たす 互いに素な自然数の組(a、b、c)に対して
d＝rad(a,b,c) とする。rad とは根基と呼ばれ下記で説明する。
任意のk>0 に対して
c>d1＋k を満たす自然数の組(a、b、c)は有限個しか存在しない
-------------------------------------------------------------------------------------
まず、互いに素とはどういう意味？ 例えばaとbが互いに素とは最大公約数が1であると同じ意味です。
gcd(28,42)＝14、 gcd(12,18)＝6、gcd(5,7)＝1
gcdは最大公約数(greatest common divisor)、根基(radical)とは
d＝rad(28,42,70)＝rad(7×22、7×3×2、7×5×2)＝7×5×3×2＝210
のように訳数を一つずつ拾えばよい。
まず簡単な例から、
(a、b、c)＝(1、2、3)とすると(a、bが決まればcは自動的にきまる)、d＝6、c＝3だから
c>d1＋k はダメだ。
(a、b、c)＝(5、7、12)とすると、d＝rad(5、7、3×22)＝5×7×3×2＝210
やっぱり、c>d1＋k はダメだ。しかし、
(a、b、c)＝(1、8、9)とすると、d＝rad(1、23、32)＝1×2×3＝6 だから、
ｋ＝0 でも、c>d1＋kは成立。
(a、b、c)＝(1、3、3)
scienceの部屋
幾何学再入門
幾何学と言えば、総ての学問の基礎というのが欧米での常識。我が国では最近あまり人気がない。化学のおける立体構造や鉱物の結晶学等、空間図形は結構ややこしい。本当はユークリッド幾何の初歩からやればよいのでしょうが、それはそのうちにKids Roomの方で展開したいと思ってます。
正四面体の重心と頂点のなす角度
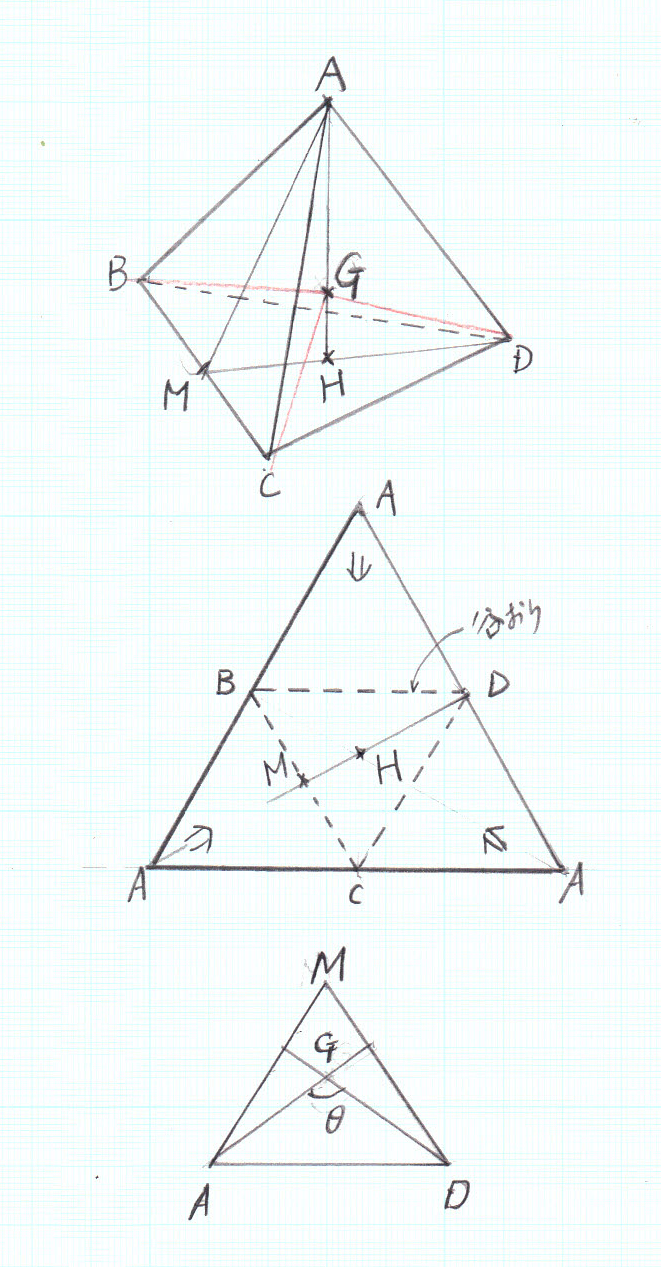メタンCH4の立体構造は、真ん中に炭素、正四面体の4つの頂点に水素分子が結合。H―C―Hのなす角度は109.5度となっています。この角度は正四面体の基本的な性質で、化学の問題でなく、自分で計算できる必要があります(化学の教科書には書いていない)。この計算は高１レベルでしょうが、立体図形でもあり結構考えにくいと思います。
まず、正四面体の重心をG、４つの頂点をA、B、C、Dとします。図を参考にしてください。下図は上の立体の展開図です。正三角形が４つ集まっています。3つのAが折り返しで一つになります。正三角形の一辺をaとします。
さて、BCの中点をMとします。
AM＝DM＝(√3/2)a
Hを△BCDの重心とすると、DH＝(2/3)DM＝(2/3)×(√3/2)a＝(√3/3)a
AH＝√(AD2－DH2)a＝√(１－(√3/3)2)a＝√6/3a
ここで、重心Gは、AH上にあって、錐体(四面体)の重心であるから、AG：AH＝3:4
よって、AG＝(3/4)AH＝3/4×√6/3a＝√6/4a＝0.6123a=(1/1.633)a
ここで、△MADを考えると、AG＝DG
求めたい角度∠AGD＝θとして、余弦定理を適用する。
2AG・DGcosθ＝AG2＋DG2－AD2
2×(√6/4)a×(√6/4)a cosθ＝(√6/4)2a2＋(√6/4)2a2－a2
∴cosθ＝－1/3
ここからは、関数電卓の出番で、cos-1θ＝arccosθ＝1.9106 rad=109.47°として求めることが出来る。
ここで、錐体の重心位置および体積の求め方をレビューする。
高さをhとして錐体(底面積S)と三角形(底辺ｂ)の比較をしてみると良く似た関係がある。でも、これ3次元と2次元の比較ともいえるけど、では4次元や1次元では？
| 図形 | 体積 | 重心位置 |
|---|---|---|
| 錐体 | (1/3)Sh | (3/4)h |
| 三角形 | (1/2)bh | (2/3)h |
数学の部屋
scienceの部屋
ベイズ統計にチャレンジ
| ベイズの定理 | ベイズ定理の確認 | ベイズ定理の拡張 | 壺でツボを押さえよう |
| どこで帽子を？ | 感染症対策 | 囚人の助かる確率 | モンティホール問題 |
ベイズ統計の定理
ベイズの定理が最近見直されているらしい。何故？ ベイズ統計というものがITの分野で使われるようになっているらしい。
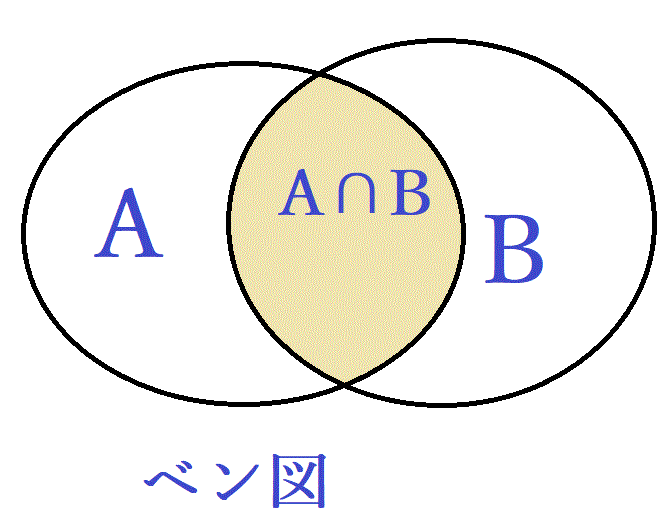まず始めにベイズの定理のもとになる条件付き確率を復習する。次の定理はベン図を描いてみれば分かる(右図)。
P(B|A)＝P(A∩B)／P(A)…(1)
これどこかでやった。1年間でA=ある感染症にかかるという事象、B=何らかの理由で死ぬという事象。A∩B＝ある感染症にかかり、かつ亡くなるという事象。
ところで、P(B|A)が条件付き確率と呼ばれるもの。Aいう事象が生じたという条件のもとでBという事象が生じる確率。P(B|A)は、感染症の致死率とも呼ばれている。
当然新型コロナウィルスにも適用できる。その例も別の項で示したのでご参考下さい。コロナウィルスで誤解されるのは、Aという事象は、PCR検査という検査を受けて陽性の結果の人だけが対象になっている。実際にはもっと感染者がいるはずだという主張は、この統計からは算出できない。
P(A∩B)＝P(B|A) P(A)…(2)
P(A∩B)＝P(A|B) P(B)…(3)
(3)は、AとBの役割を交換しただけで、これもベン図から納得できる。
(2)(3)の左辺は同じ。 ∴ P(A|B) P(B) ＝P(B|A) P(A)
これを、P(A|B)＝P(B|A) P(A)／P(B) …(4)
P(A|B) をP(B|A)の逆確率と呼ぶようだ。
Aが起こった時Bが起こる確率P(B|A)に、Bが起こった時Aが起こる確率P(A|B)を対応させる式。
コロナに感染(A)して死ぬ(B)確率に、死んだ時にそれがコロナである確率を対応させるということか。
実際の応用の場面では、(4)式でAを原因、Bを結果と考えることが多いようだ。
だからP(A|B)を原因の確率 とも呼ぶ。
また、P(A)を事前確率、P(A|B)を事後確率 とも呼ぶ。
名前が、どれが原因でどれが結果かなんだか結構ややこしい。
ベイズ統計にチャレンジ
scienceの部屋
ベイズ定理の確認
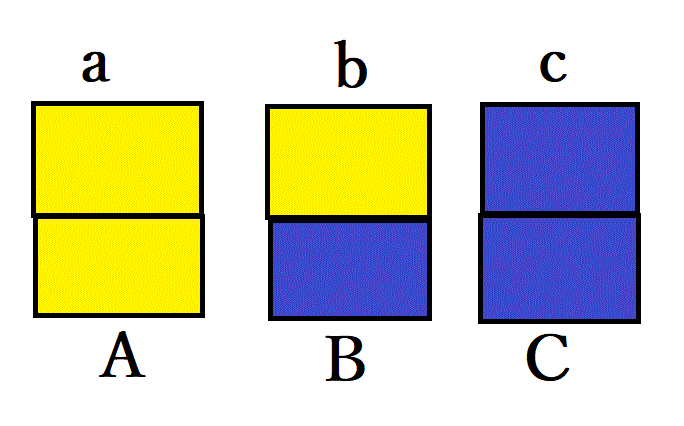ベイズ定理の確認を確認するための簡単な例題。
箱の中に3枚のカードa、b、c が入っている。カードa は両面が黄色、ｂは黄と青。ｃは両面が青だ。
さて、カード1枚を取り出し机の上に置いた。取り出したカードの上面が黄色であったとしたら、そのカードがｂである確率は？？
A、B、Cをカードa、b、c が取り出される事象とする。また、Y、Sを取り出したカードの上面が黄、青である事象としよう。
求めたい確率は、条件付き確率の記号を使って、P(B|Y)となる。
この確率は、普通の確率の定義から簡単に求まる。P(B|Y)となる事象は次の3つの場合しかない。つまり、a表、a裏、b表の3つの場合しかない。しかも、この3つの場合は同様に確からしいと言える。従って、P(B|Y)＝1/3
次にベイズの定理
P(B|Y)＝P(Y|B)P(B)／P(Y) …(1)
カードを取り出す総ての場合を列挙すると、
→→①aの表黄、②aの裏黄、③bの表黄、④bの裏青、⑤cの表青、⑥cの裏青の6通り
従って、P(Y)＝3/6＝1/2、P(B)=1/3 、P(Y|B)＝1/2
であることは、図からも明らか。
これを(1)に入れて、P(B|Y)＝(1/2)( 1/3)／(1/2)=1/3
当然とはいえ、一致する。
ここで、カードを選択することは、色の原因であり、色はその結果と解釈する。色という結果から、その原因であるカードを選択する確率を求めている。だから、得られた結果を「原因の確率」と呼ぶのかベイズ流の考えらしい。
ベイズ統計にチャレンジ
scienceの部屋
ベイズ定理の拡張
以下は、ベイズの定理 P(A|B)＝P(B|A) P(A)／P(B) …(1)
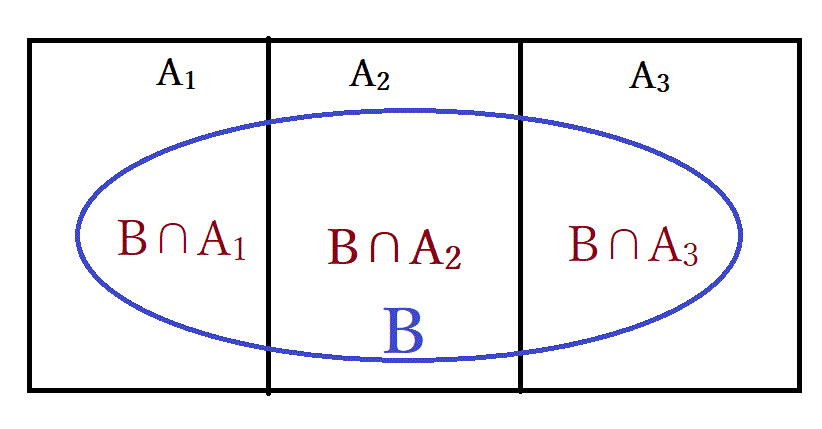
に多少の変形を加えたもの。右図を見て下さい。A＝A1＋A2＋A3 つまり、Aは共通部分の無い3つの部分から（排反事象）なっています。
また、B＝B∩A1＋B∩A2＋B∩A3
ところで、ベイズの定理もこの場合、P(Ai|B)＝P(B|Ai) P(Ai)／P(B)
(ただし。i＝1～3) …(2)
従って、確率P(B)は、P(B)＝P(B∩A1)＋P(B∩A2)＋P(B∩A3) と表わせる。
右辺の各項に乗法定理を適用する。
P(B)＝∑P(B∩Ai)＝ΣP(B|Ai)P(Ai) (∑はi＝1、2、3の和)
これを(2)に代入すれば、
P(Ai|B)＝P(B|Ai) P(Ai)／∑P(B|Ai)P(Ai) (ただし。i＝1～3) …(3)
先の例題に(3)式を用いた場合。
箱の中に3枚のカードa、b、c が入っている。カードa は両面が黄色、ｂは黄と青。ｃは両面が青だ。 さて、カード1枚を取り出し机の上に置いた。取り出したカードの上面が黄色であったとしたら、そのカードがｂである確率は？？
【解】
求める確率は、取り出しがカードが黄だった時、それがb(B)である確率、つまりP(B|Y)が欲しい！
(3)式を利用すると
P(B|Y)＝P(Y|B)P(B)／{P(Y|A)P(A)＋P(Y|B)P(B)＋P(Y|C)P(C)} …(4)
この式が何故便利か？図を見て考えて見れば分かる。
① P(Y|A)＝1 → aのカード取り出され時、それが黄色の確率
② P(Y|b)＝1/2→b のカードが取り出されたとき、それが黄色の確率
③ P(Y|C)=0→c のカードが取り出されたときそれが黄色の確率
また、P(A)＝P(B)＝P(C)＝1/3 （∵3枚のカードから1枚を取り出す確率は同様に確からしい）
これを(4)式に代入すれば、答えが求まる。
P(B|Y)＝（1/2×1/3)／(1×1/3＋1/2×1/3＋0×1/3)＝1/3
当然ではあるが、これは先ほど求めた結果と一致している。
ベイズ統計にチャレンジ
scienceの部屋
壺でツボを押さえよう
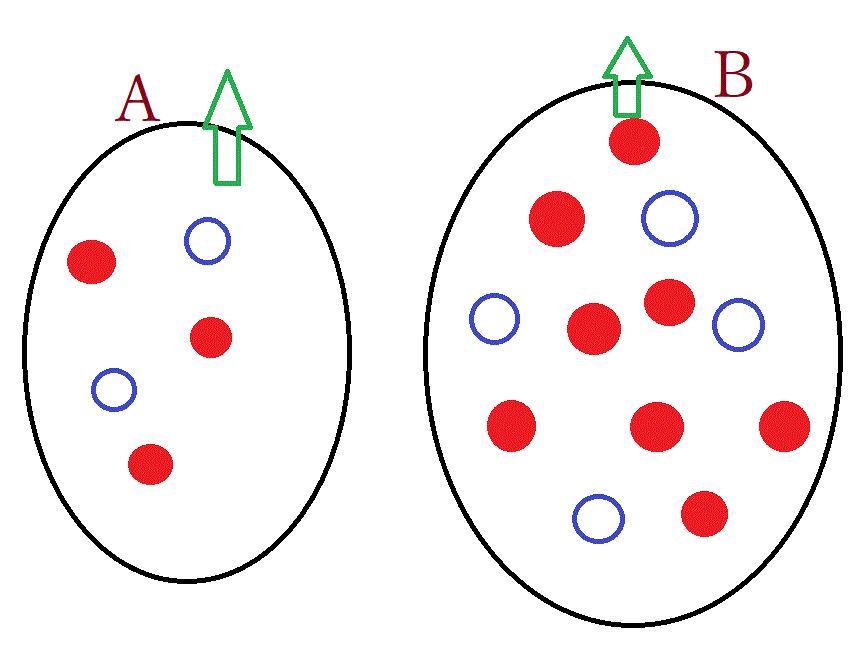【例題1】2つの壺 a、b がある。a の壺には赤玉3個、白玉2個入っている。b の壺には赤玉8個、白玉4個入っている。壺 a、b が選ばれる確率は、1：2 とする。今、どちらかの壺から玉1個取り出したら、赤玉であった。その赤玉が a から選ばれている確率は?? b から選ばれている確率は??
【解】
事象を次のように決める。
A: 壺 a から玉を取り出す。B: 壺 b から玉を取り出す。R: 取り出した玉が赤玉であった。
求める確率は P(A|R)となることは分かる？
ベイズの定理((3)式)から、
P(A|R)＝P(R|A)P(A)／{P(R|A)P(A)＋P(R|B)P(B)} …(1)
P(A)＝1/3、P(B)＝2/3 (∵壺aと壺bが選ばれる確率は1：2)
また、P(R|A)＝3/5、P(R|B)＝8/12＝2/3、これを上の式に代入すれば簡単。
P(A|R)＝(3/5)(1/3)／{(3/5)(1/3)＋(2/3)(2/3)}＝9/29
同様にして、
P(B|R)は、
P(B|R)＝P(R|B)P(B)／{P(R|A)P(A)＋P(R|B)P(B)} …(1)
P(B|R)＝P(2/3)(2/3)／{(3/5)(1/3)＋P(2/3)P(2/3)}＝20/29 …(1)
P(A|R)＝9/29、P(B|R)＝20/29、出た玉が赤玉であった時、それは壺aから壺bからのどちらかでしかないから、P(A|R)＋P(B|R)＝1となります。
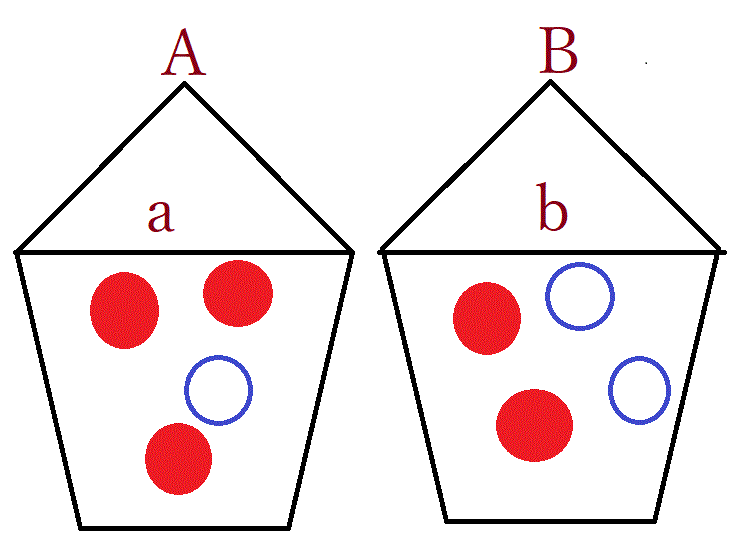【例題2】外見からは全く区別がつかない2つの壺 a、b がある。a の壺には赤玉3個、白玉1個入っている。b の壺には赤玉2個、白玉2個入っている。今、どちらかの壺から玉1個取り出したら、赤玉であった。その赤玉が a から選ばれている確率は?? b から選ばれている確率は??
【解】
外見からは全く区別がつかないということは、P(A)＝P(B)＝1/2としてしまいます。これを理由不十分の法則と呼んでいる。
P(A|R)＝P(R|A)P(A)／{P(R|A)P(A)＋P(R|B)P(B)} …(1)
＝(3/4)(1/2)／{(3/4)(1/2)＋(1/2)(1/2)}＝3/5=0.6
P(B|R)＝P(R|B)P(B)／{P(R|B)P(A)＋P(R|B)P(B)} …(1)
＝(1/2)(1/2)／{(1/2)(1/2)＋(1/2)(1/2)}＝3/5=0.5
ベイズ統計にチャレンジ
scienceの部屋
どこで帽子を？
5回に1回、帽子を忘れて来てしまう、営業マンの王さん。正月年始回りで得意先をA、B、Cと3軒を順に回って家に帰って来て、帽子を忘れたことに気がついた。2軒目のB社に忘れて来た確率は？br>
これ、大学入試(早稲田)にも出題された難問らしい？
家を出るときには帽子を確かに被っていて、帰った時には無かった。途中の記憶はないということか。
まず、事象A、B、C、Fを
A: A社に入る時には帽子を持っていた。/B: B社に入る時には帽子を持っていた。/C: C社に入る時には帽子を持っていた。/F: 家に帰って帽子を忘れたことに気がついた。
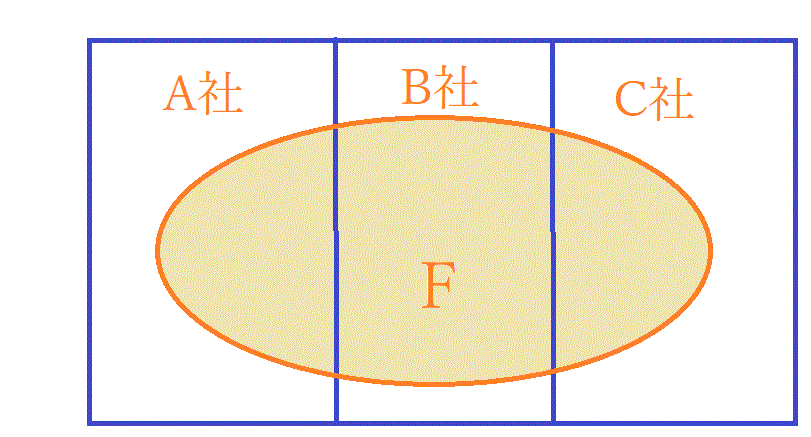
集合に使うベン図を描いてみた。
どうも事象A、B、Cは一見排反事象ではないようだが。ただ、このように事象を設定すれば3軒を回る順番は問題にならないようにも見える。
求める確率は、P(B|F)
P(B|F)＝P(F|B)P(B)／{P(F|A)P(A)＋P(F|B)P(B)＋P(F|C)P(C)} …(1)
P(F|A)＝P(F|B)＝P(F|C)＝1/5、P(A)＝1、P(B)＝4/5、P(C)＝(4/5)2＝16/25
P(B|F)＝(1/5)(4/5)／{(1/5)(1)＋(1/5)(4/5)＋(1/5)(16/25)}=20/61
同様にして、P(A|F)＝(1/5)(1)／(61/125)＝25/61、 P(C|F)＝(1/5)(16/25)／(61/125)＝16/61(1)
P(A|F)＝25/61、P(B|F)＝20/61、P(C|F)＝16/61 となり、P(A|F)＋P(B|F)＋P(C|F)＝1
A、B、C 3社のうちのどれかだから、確率の合計が1になるのは当然だが、先に尋ねた会社ほど確率が大きくなるのはチョット意外かも。事象A、B、Cの生ずる確率が異なるためだ。
ベイズ統計にチャレンジ
scienceの部屋
感染症対策
ある病気を発見するT検査法に関して、次のことが知られている。
①病気にかかっている人に、この検査を行えば98％の確率で病気であることが正しく診断される。見逃すのはたったの2％。
②病気に罹っていない人に、T検査を実施すると、5％の確率で誤って病気にかかっていると診断される。
③母集団においては、病気にかかっている人の比率は3％、つまり97％の人は健常者ということ。
98％の確率と謳っているこの検査法、どのくらい信頼できるのでしょうか。
【普通の確率的手法】
母集団として、仮に10000人（1万人）とする。すると、
・病気に罹っていない健常者の人数＝10000×0.97＝9700人
・病気に罹っている人の人数＝10000×0.03＝300人
これが母集団ということだが、
・健常者が病気と診断される人数＝9700×0.05＝485人
・病気に罹っている人が本当に病気と診断される人数＝300×0.98=294 人
・T検査で病気と診断される人数＝485＋294＝779人
従って、T検査で病気に罹っていると診断される人が、本当に病気に罹っている確率は、
病気に罹っている人が本当に病気と診断される人数／T検査で病気と診断される人数＝294／779＝0.377→約38%、残りの62％は健常者なのに病気と判断されてしまうことに。
この結果、大変驚きですね。98％の確率と言われれば医師も患者も、つい信頼してしまうでしょうが。半分以上が誤判断。一番騙されやすいのがマスコミ関係者や政治家のようですが。
がん検診なんかで、やたらと癌の可能性ありも不安で困るけど、見逃されてしまうのも怖い。検査の前にどう診断されるのか確率をはっきりさせて欲しいね。ところで新型コロナのPCR検査はどうなのでしょうか。なんせ判断基準はこれしかないのだから。この確率が分からないと検査を受けるのも怖い。何ら症状がないのに陽性だから感染者と言われても、かなりの人は本当は陰性かも知れない。この辺は検査担当者も口にマスクで秘密の話だろうが。
【実際に試して見よう】
新型コロナウィルスの感染者を発見するPCR検査法に関して、次のことが知られている。
①感染している人に、この検査を行えば98％の確率で感染者(陽性者)であることが正しく診断される。見逃すのはたったの2％。
②感染していない人(陰性者)に、PCR検査を実施すると、5％の確率で誤って感染者(陽性)だと判断される。
③母集団においては、感染者の比率は3％、つまり97％の人は健常者(陰性者)ということ。
98％の確率(例えばに話し実際は？)と謳っているPCR検査法、どのくらい信頼できるのでしょうか。
母集団として、仮に10000人（1万人）とする。すると、
・感染していない健常者の人数＝10000×0.97＝9700人
・実際感染している人の人数＝10000×0.03＝300人
これが母集団ということに、
・陰性者が陽性と診断される人数＝9700×0.05＝485人
・陽性者が本当に陽性と診断される人数＝300×0.98=294 人
・PCR検査で陽性と診断される人数＝485＋294＝779人
従って、PCR検査で陽性と診断される人が、本当に陽性である確率は、
陽性者が人が本当に陽性とされる人数／PCR検査で陽性と診断される人数＝294／779＝0.377→約38%、残りの62％は健常者(陰性)なのに感染者(陽性)と判断されてしまうことに。これ大変なことだ。PCR検査で陽性だと言われても、この例では半数以上は実際は健常者(本当は陰性)ということだから。実際はどうなのか調べて見たくなりますね。
【ベイズの定理を使った解法】
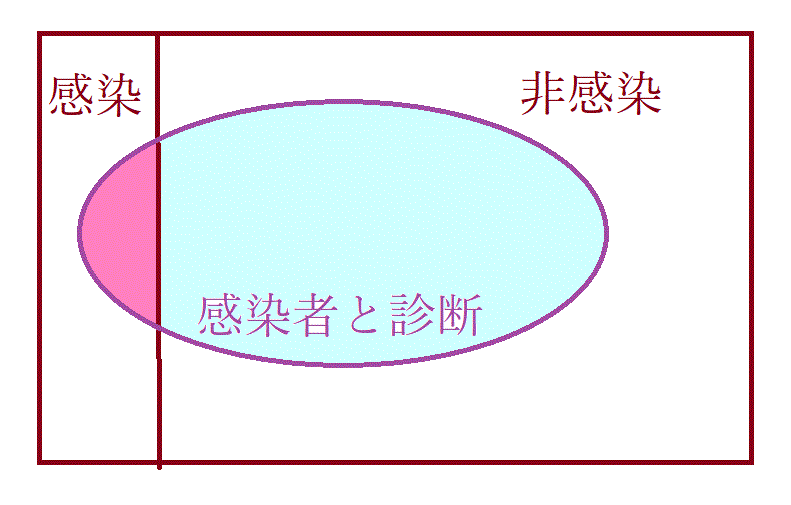
事象の整理→U＝母集団、A=感染者、AC＝健常者、A∩AC＝∅、B＝感染症と診断
求めたい確率は、P(A|B)、 するとベイズの定理から
P(A|B)＝P(B|A)P(A)／{P(B|A)P(A)＋P(B|AC)P(AC)}
となり、P(A)＝0.03、PAC)＝0.97、P(B|A)＝0.98、P(B|AC)＝0.05
∴ P(A|B)＝ (0.98) (0.03)／{ (0.98) (0.03)＋ (0.05) (0.97)}＝294／(294＋485)＝294/779＝0.377→約38％
これを見るとベイズの定理を使った方が、分かり易いかも知れない。
【追記】
感染症でも、今流行の新型コロナな場合は厄介でしょうね。感染者の数が皆目見当がつかない。PCR検査で陽性の者をとりあえず感染者としているらしい。検査の精度も100％でには及ばないらしいし。しかし、潜伏期間を過ぎると一時的に陽性のものも何事もなく陰性に転じて健常者に。PCR検査は、感染症を疑われ症状を呈している人には必要な検査だ。しかし、これで感染の実態がどうだなんている話になると？？？という感じですね。実際、感染者の数がいくら増えても死者や重症者が少なければ問題ない。適切な治療法がない現状では、むやみに検査数増やしても何の意味もないかもね。
ベイズ統計にチャレンジ
scienceの部屋
囚人の助かる確率
「3人の囚人の問題」というのはちょっとしたパラドックスのような問題です。
3人の死刑となる囚人がいた（A、B、C）。一人だけ恩赦されることに。恩赦される囚人は無作為に選ばれる。誰が恩赦されるか看守だけが知らされている。そこで囚人Aは、看守を買収して言った。「BとCのどちらかは必ず処刑されるんだ。どちらが処刑されるかを教えてくれ。それなら私に情報をくれたことにはならないだろう。」看守は考えた。「うん。それなら教えたことにはならないね。処刑されるのはBだよ。」
囚人Aは、考えた。「初めは自分が処刑されずに助かる確率は1/3だった。でも今度は処刑されるのは自分かCだ。助かる確率は1/2に増えた。」買収の成果はあったと言えるのでしょうか。
【解】次のように事象を定義する。 A: Aが助かる。B: Bが助かる。C: Cが助かる。
SA: Aが処刑されると看守から教えてもらう。SB:Bが処刑されると看守から教えてもらう。SC: Cが処刑されると看守から教えてもらう。
Bが処刑されると教えられたという条件の下で、Aが助かる確率は本当に1/2になるのでしょうか。
【解】
まず、P(A)＝P(B)＝P(C)＝1/3、看守の言ったことから、P(SB｜B)＝0、P(SB｜C)＝1、
P(SB｜A)＝1/2
求める確率はP(A|SB)であるから
P(A|SB)＝P(SB｜A)P(A)／{ P(SB｜A)P(A) ＋P(SB｜B)P(B)＋ P(SB｜C)P(C)}
＝ (1/2) (1/3)／{ (1/2) (1/3) ＋ (0) (1/3)＋ (1) (1/3)}
＝1/3
結局、Aが助かる確率(1/3)は変わらないんだ。当たり前なのか、チョト不思議な気もする。情報を得て得したような気になる実際は無意味だった。
ベイズ統計にチャレンジ
scienceの部屋
モンティホール問題
これは名前がついていることからかなり有名な問題らしい。
3つのドアーがあり、そのうちの一つに賞金が隠されているとのこと。そのドアーを開ければ賞金を貰える。ドアーをA、B、Cとしよう。まず、解答者はドアーの一つを選ぶ。これをAとしよう。すると正解を知っている出題者(或いは司会者)は、残りの2つのドアーの一つを開けて、「このドアーは違います。」と言って外れのドアー（これをCとする）を開ける。
ここで、解答者は残りの2つのドアーのいずれかを選び直す権利を与えられる。つまり、元の選択のAのままにするか、Bに変更するかだ。どちらを選択する方が当たる確率が高いのだろうか？ もちろん正解は不明だけど確率の高い方を選択する方が有利なはずだね。
もう一度確認をすると、
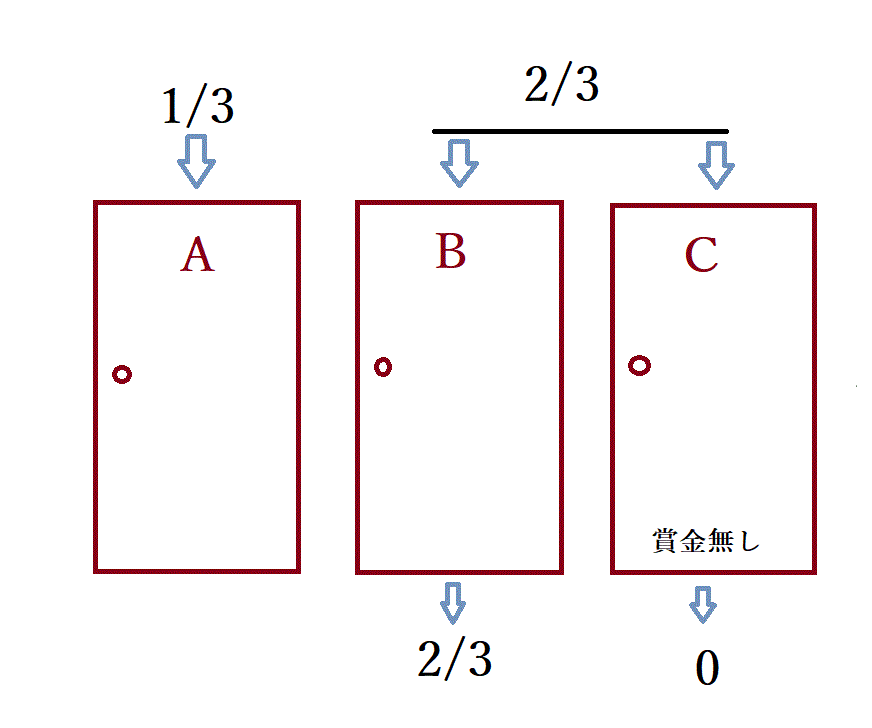
① 3つのドアーのどれかにランダムに賞金が入っている。つまり確率は1/3。
② 出題者は賞金のあるドアー(答え)を知っている。もし回答者が正解のドアーを選んでいれば、残りの2つからランダムに一つを開ける。もし回答者が不正解のドアーを選んでいれば、出題者は賞金の入っていない方のドアーを開ける。
【解答】
事象を次のように決める。A ; ドアーAが当たり、B ; ドアーBが当たり、D；ドアーCが開けられる。
求めたい確率は、P(A|D)、P(B|D)、ベイズの定理を用いて、
P(A|D)＝P(D|A)P(A)／｛P(D|A)P(A)＋P(D|B)P(B)｝＝1/3
P(B|D)＝P(D|B)P(B)／｛P(D|A)P(A)＋P(D|B)P(B)｝＝2/3
(∵ P(A)＝P(B)＝P(C)＝1/3、P(D|A)＝1/2、P(D|B)＝1 )
つまり、Bを選んだ方が当たる確率が2倍も高くなる。
ベイズ統計にチャレンジ
scienceの部屋
ベクトル解析入門
水理学や流体力学において、ベクトル解析の知識は極めて重要である。そういう私も、水理学はEulerの運動方程式やベルヌーイの定理程度の基礎でものたりたわけで、何を今さらということもありますが、ベクトル解析自体が流体の本質を解明するために発展して来たものなのです。ちょうど、微分積分の発展が質点系の力学と一緒に車の両輪のように発展してきたことと全く同じです。更に、電磁気学も電荷の流れをちょうど流体として扱うため、ベクトル解析の理解が不可欠なのです。最終的には、電磁気学のマクスウェルの式まで到達したいと思います。現象をどのような式で表現するかは現象を理解するうえで極めて大切です。そのため、若干の寄り道をしてベクトル解析の基礎をマスターしたいと思います。
まずは、一番良く見かけるgrad, div, rotについて。これを見ただけで逃げ出してしまう人もいるかも。三つとも同じ記号では∇と書きます。一種の微分みたいなもの。ただし、これは数値ではなく、いわゆる演算子というもの。ちょうどd/dxとか∂/∂xと同じ。すなわち、∇＝(∂/∂x, ∂/∂y, ∂/∂z)です。これは、3成分を持った1種のベクトル見たいなもの。∇f=grad f。つまりスカラー関数f(x,y,z)にかければ、ベクトル×スカラーで結果はベクトル。勾配と呼びます。∇・A＝div A。ベクトルAに内積として掛ければ、結果はスカラーで発散と呼ばれます。最後に∇×A＝rot Aは、回転と呼ばれ、外積なので結果はベクトルです。
また、∇を組合わせた次の公式も重要です。
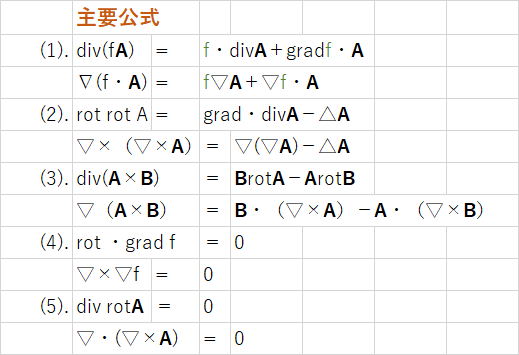
ベクトルに関する積分の公式もあります。
部分積分と置換積分
物理や理工系の専門書を頻繁に数式が出て来ます。
【部分積分】部分積分
関数f(x)とg(x)がある時、
∫f g’ dx＝f g－∫f’ g dx …(1)
これが、部分積分の基本公式。
例えば、I＝∫log x dxを求めたいとします。
この時、f＝log x、g＝ｘと置きます。ｆは積分は出来ないけど、微分したら1/xとなります。
gは微分すると1です。
I＝∫log x dx＝x log x－∫(1/ｘ)ｘdx ＝x log x－ｘ＋Ｃ …(2)
(1)式のもとは、微分法の積の微分公式 (f・g)＝f’g＋f g’ です。
【置換積分】置換積分
関数f(x)とg(x)がある時、g(f(x))の積分を考えます。
∫g’(f(x)) f’(x)dx＝g(f(x))＋C …(1)
これも、微分法の合成関数の微分からきています。
(g(f(x)))’＝g’(f)・f’ ; 全体をｆで微分して、次にｆをｘで微分します。
(1)では、迷わずにf(x)＝hとおいてみます。f’(x)＝dh/dxだから、
∫g’(h)) (dh/dx)dx＝∫g’dh＝g(h)＋C
数学の部屋
ベイズ統計にチャレンジ
scienceの部屋