力学も面白い

力学と言えば、物理学のもっとも基本。だから、色々な現実の諸現象を理解しようと思えば、やはりある程度の知識は必要。実はゴルフの力学なんて立ち上げて、やっぱり大変なことを実感している。今までScienceの部屋で取り上げた話題も含めて少しずつ充実させていきたいと思っています。

目次 　

円運動	回転する剛体	斜面を転がるビール樽	回転する座標系
静水圧とは	マグデブルクの半球	ロケットは何故飛ぶのか	ロケット(2)	地上から発射
地球の引力	宇宙速度	中心力による運動	中心力による運動(2)	惑星の軌道
ケプラーの第3法則

水理学再入門
複素数と流体力学
ゴルフの力学

円運動

学校の物理では、直線運動が多くて回転系に関してはやや手薄だったような気がします。ゴルフのスィングから人工衛星の運動まで、回転系を理解することは重要でしょう。また、ボールと茶筒が斜面を転がる時、どちらが先に落ちるか、すぐに答えられますか。台風の進路が曲がるコリオリの力、色々と面白い話題がありそうです。
    直線運動の次に簡単なのが円運動でしょう。「円（縁）は偉なもの味な物」何て言うが、そう一筋縄ではいかないようだ。一番簡単に出来る実験は紐の先に重りをぶら下げてぐるぐる回せばいいのだが。
     まず、直線運動と違って、変数が(x,y)と2つになる。実は、円運動は、これを円盤として横から見ると、単振動なのだ。x方向もy方向も単振動、そしてその位相が90°ずれている。

円の中心Oから、円周上へのベクトルを考える。円の半径は r とする。→r＝(x,y)＝(r cosθ, r sinθ)、   ここで x²＋y²＝r²
重（おも）りをぐるぐる回すと、重りは紐と反対の方向に飛んでいこうとする力が働く。遠心力だ。飛んでいかないようにするために紐にも力を加えないといけない。これを向心力と言う。遠心力と向心力が釣り合っていることで円運動が持続する。
円の中心Oから、円周上へのベクトルを動径ともいう。考えている質点m は円周上にあるので、その位置は最初の位置からの回った角度だけで決る。角度はθ＝ω t＋θ₀ と表わされる。ここで等速円運動を考えると、dθ／dt＝ω（一定）で、このωを角速度という。直線運動の速度に対応するものともいえる。円周方向の速度は、v＝rωとして表される。
動径ベクトルを2回、時間で微分したもの加速度、これに質量 m をかけたものが質量に作用する力に等しいのはニュートンの法則（F＝m a）だ。回転する質量 m は、常に動径の向きと反対方向の力を受けている訳でこの力を向心力という。向心力と良く誤解されるのが遠心力。向心力と遠心力は大きさが同じで方向が反対の作用と反作用みたいな関係ですが、少なくとも左の図を見ていても質点 m にはそのような力は働いていない。でも、あなたが質点 m にいて一緒に動いていれば外向きにそのような力を感じるはずだ。つまり回転する座標系に対して生じる見かけの力と言われるもの。一般相対性理論まで学べば力には本当の力と見かけの力の区別はないと言われている。

力学も面白い

円運動の一例として円錐振り子と言うものがある。天井から重りをぶら下げただけのものだが。普通の振り子と同じなので、黙って重りを放すと振り子時計と同じ普通の振り子だ。円運動にするにはチョット工夫がいりそうだ。また楕円や他の図形になることはないのでしょうか。頭の中で考えるなら簡単ですが。
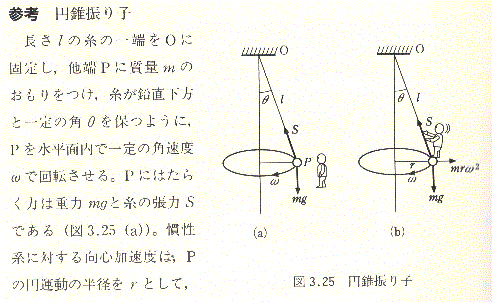     点P（m）に働く力は鉛直下向きの重力（mg）と上向きの糸の張力S。上向きにはScosθ＝mg…①、向心力としてはSsinθ＝mrω²…②、  また、r＝lsinθ、
②→Ssinθ＝lsinθ・mω²→S＝lmω²→lmω²cosθ＝mg　、  ω²＝g/lcosθ

     ω＝√ （g／lcosθ）→T＝2π／ω＝√ （lcosθ／g）
最初にv＝rωとなるような速度で回転させればこのような振子になりそうだ。

力学も面白い

回転する剛体

質点の回転の次には剛体の回転を考えねばならないでしょう。
   
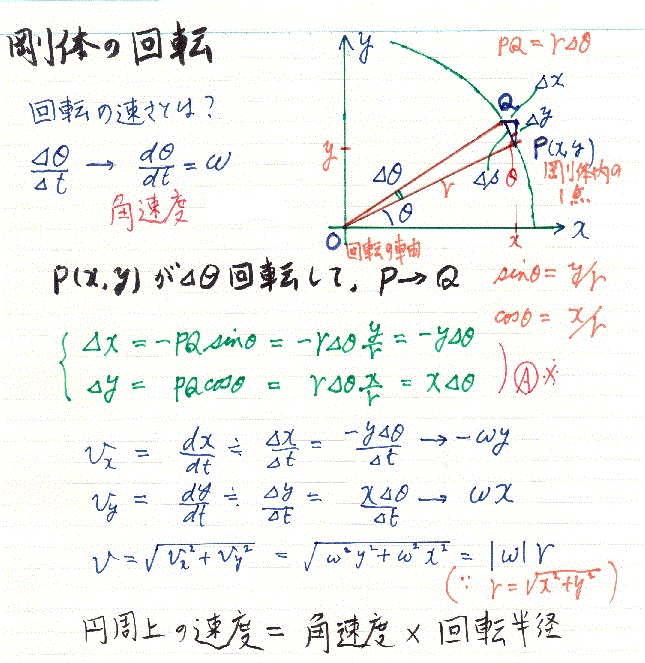
回転の速さを表すには、角速度を使います。単位時間にどれだけの角度を回ったかということ。角度の単位にはラジアンを使います。円周を1回転して2π  radian、これに半径をかけると円周の長さになります。ラジアンの単位は表記されません。つまり無次元なのです。円周上の実際の速さは、角速度に半径を掛ければ求められます。
次の微小変化の関係が活躍します。点Pが角度△θだけ回転して点Qまで動いた時の、x-y座標の変化です。
    △x＝－PQ sinθ＝－r△θ (y／r)＝－y△θ
    △y＝PQ cosθ＝r△θ (x／r)＝x△θ


    回転の場合は、回す力、すなわち力のモーメントを考えないといけません。考えなければいけない力は、円周に接する方向です。力のモーメントのことをトルクと呼んでいます。
トルクに回転角をかけるとこれが仕事になります。力に動いた距離を掛けたのが仕事になるのと同じ理屈です。この時力の向きと回転の動径の向きが一般には一致してないので一工夫必要です。
△W＝F_Ⅱ△s(＝｜F｜d)＝F_Ⅱr△θ＝T△θ
左の図を見れば分かるようにF_Ⅱrはトルクです。故にこの時の仕事はトルクに回転角をかけたものであることが分かります。一方、仕事は力に動いた距離をかけたものでありました。→△W＝F△s＝F_x△x＋F_y△y＝（xF_y－yF_x）△θ
ここで最後の式には上で求めた、（△x , △y）＝（－y△θ , x△θ）の関係を用いています。
従って、トルクはT＝xF_y－yF_x
F_x＝m d²y／dt²   及び   F_y＝m d²x／dt²の関係を利用すると、 これからトルクと力の関係が求まります。
T＝x m d²y／dt²－y m d²x／dt²

    
一方、L＝x m dy／dt－y m dx／dtとおいて、このLを微分するとT（トルク）になることが求められます。このLを角運動量と言います。
すなわち、T＝dL／dt、トルクは角運動量の時間変化で示されます。ちょうど、力は運動量の時間変化F＝dp／dtで表わされることに対応している。
また、L＝x m dy／dt－y m dx／dt＝x p_y－y p_x  となることから、
L=r × p   という表示が出来ますが、これはベクトルの外積を用いたもの。角運動量がベクトルになるというのも、チョット分かりにくい気がしますが、回転面に対して垂直で右ねじの進む方向を正とするベクトルと考えることもできます。このようンベクトルを軸性ベクトルというそうです。
次の、直線運動と回転運動の次の対応はしっかり把握しましょう。
速度～角速度、力～トルク、運動量～角運動量、質量～慣性モーメント
一方、角運動量はL＝m v rと表わすこと出来ます。運動量に腕の長さをかけたもので、この形の方が良く使われるかも。証明は極座標に変換して左に示したようにできます。　

剛体の中の質点は角運動量L＝m r v＝m r ω²  の角運動量を持っている。剛体内の各部分はどこでも角速度が一定でだけれどもその速度は軸から遠くなるほど大きくなる。だから全体の角運動量は、L=Σ(m_ir_i²)ω  と表わされる。
ここで、I＝Σm_ir_i²  を慣性モーメントと称する。連続体を考えた場合は、積分表示で　I＝∫_vρr²dv  となる。慣性モーメントは質量と違い軸の取り方で異なり、物体の変形によっても変わってしまう。 【回転する剛体のまとめ】
1.回転の速さは、角速度を用いる。角速度は進んだ角度を要した時間で割ったもの。
2.角速度をω、回転した角度をθとすると、ω＝dθ/dt
3.円周上の速度＝回転半径×角速度
4.トルクとは力のモーメントのことで、トルク＝力×腕の長さ。ただし、力の向き、腕の長さの計り方には要注意。T＝F∥×r＝F×ｄ。
5.力は運動量の変化として表せるのと同様に、トルクは角運動量の変化として表せる。
すなわち、F＝dp/dt、T＝dL/dt

6.角運動量は、L＝mrvともできる。つまり、L＝pr
7.剛体の慣性モーメントはI＝∑(m_ir_i²)ω、角運動量＝Iω
8.角運動量＝慣性モーメント×角速度　(運動量＝質量×速度)
9.固定軸を持った剛体の回転運動の方程式
　T＝Idω/dt＝Id²θ/dt²

力学も面白い

斜面を転がるビール樽

斜面でビー玉を転がす、空き缶(かん)を転がす。小さな子供の大好きなあそび。だけど空き缶(かん)と、ジュースの詰まった缶どちらが先に落ちるか。ビー玉とおもちゃの自動車では。大抵は同時でない。でも正解は大人が考えても結構難しい。
ビー玉は転がる。サイコロは滑(すべ)る。でも斜面の傾斜を急勾配にすればビー玉も滑るのではないかな。斜面が垂直までたつと今度は自由落下。
ところが、昔ガリレオ・ガリレイは自由落下の研究をするのに斜面を使って行ったと言われる。だって当時に時計の能力では、自由落下は速すぎて計測できない。因みに光速の測定も試みたが、もちろん速すぎて計れなかった。でも、自由落下は回転しないでストンと落ちるのに斜面ではコロコロと転がって落ちる。果たして同じ物理法則に従っているんでしょうか。

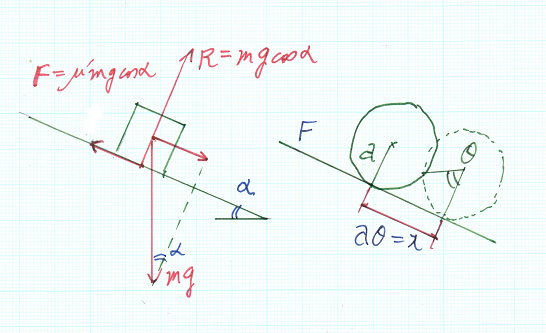
まず、図に示すように斜面に物体を置いて見ます。初等物理学の最初の方にある絵ですね。座標軸は、斜面に沿って下向きにxと取りましょう。傾斜角をαとします。
物体がサイコロなら転がらずに傾斜が急になると下向きに滑り出すでしょう。この時物体に働く力は重力だけです。斜面に垂直方向の力は、mg cosα、この力の成分は斜面から物体への抗力Rと釣り合っているので運動には関係しません。斜面に沿ったx方向の力だけを考えればいいですね。下向きの力はS＝mg sinα、これに抵抗するのが摩擦力       F＝μR＝μmg cosα
結局S>Fとなれば、物体は滑り出します。だから滑らずに安定する条件は、
μmg cosα＞mg sinαだから、μ＞tanαとなれば良いことになります。μは静止摩擦係数と呼ばれる係数で物体の面の粗さなどで決まるため理論的に算出することは出来ません。動き始めると動摩擦係数μ´に変わるため少し小さくなって動きやすくなります。動き始めると急に軽くなったように感じることからこれは理解できます。摩擦係数が0の場合は、斜面に沿って下向きの力がmg sinαだけとなり、自由落下の条件でゆっくりと落下しそうですね。ガリレオが求めていた実験用の斜面はこれですね。ドライアイスや氷で斜面を作れば摩擦を0には出来ないものの無視できる程度に小さくできるでしょう。しかし、ガリレオの時代ではまず不可能。そこで斜面を転がしたらどうかと考えるのは当然でしょう。
斜面を転がる物体は、球か円筒か。ただ気をつけないといけないのは本当にいつも転がってくれるのか、転がりながら同時に滑ることはないのか。そして、本当に斜面の実験結果から自由落下の場合が極限(α＝90°)として計算できるのか。自由落下については、我々は既に学校で習っているけれど、これは後知恵で、ガリレオ自身はは斜面実験から自由落下を推定したのですよね。また、球や円筒でも中空の場合はどうか、中に水などの流体を詰めた場合は等々色々な疑問が出て来ます。
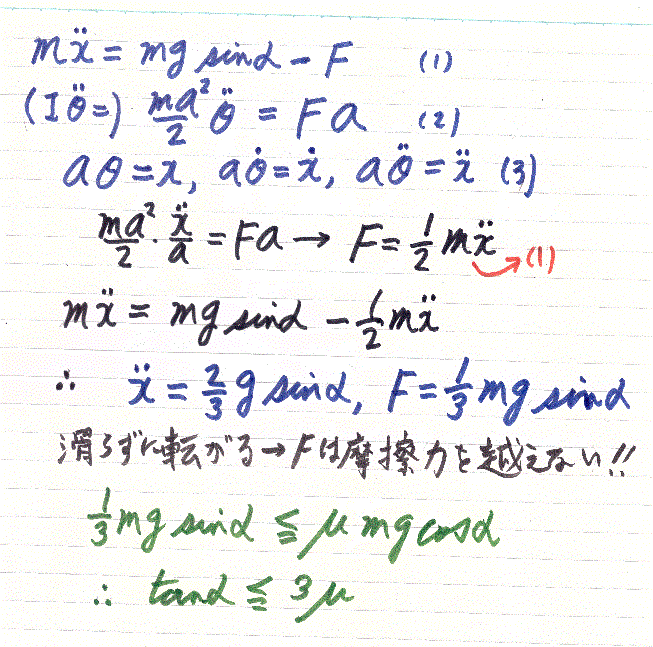まず、斜面が緩い場合は、滑ることなく転がるものと考えられます。まず、2次元的に考えて円筒を考えます。半径aの円筒が転がって距離xだけ進むとします。左に示した式①～③を参照して下さい。この時円筒の回転した角度θとすると、aθ＝xの関係が成立します。
上の式で少し分かりにくいのは②の式です。  Id²θ／dt²＝F a
これが回転する剛体の運動方程式です。右辺のF a は力のモーメント、すなわち回す力＝トルクです。Iは慣性モーメントいうもので I＝∫_V（ρr²）dVとして積分を用いて計算されます。
球や円筒のような回転体では、I＝Cma²とすると(Cを形態因子、a半径、ｍは質量)とすると、Cの値は、リングでC＝1、円筒(円柱)でC＝1/2、球でC＝2/5、球殻でC＝2/3となるようです。Iは、直線運動の際の動きにくさ、つまり質量に相当するもので、Cが小さいほど回転しやすいことを表します。つまり、球(C＝0.4)は円筒(C＝0.5)より若干速く転がることが分かります。


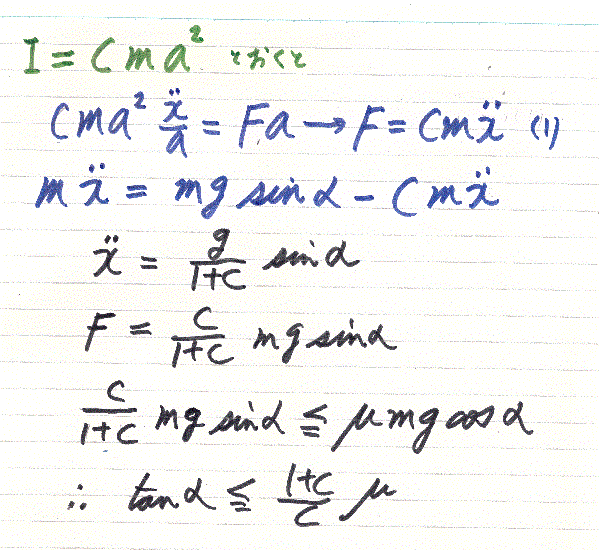
上の円筒の計算を一般化して、Cを使って計算すると下記のようになります。xの二回微分から加速度が求まるので、これを自由落下のgと見做すと斜面での運動は分かります。ただし自由落下と異なり形(円筒とか球）で微妙に加速度が異なります。左の最後に求めた不等式の条件は物体が滑らず転がる条件。さて、今度は滑りがある場合、つまり摩擦が小さいか斜面が急な場合を考えないといけませんね。

力学も面白い

回転する座標系

回転する座標系にのった観測者から見ると、見かけの力が働きます。有名なものとして遠心力とコリオリの力。特にコリオリの力は教養の力学ではあまり触れられていないので分かりにくい所があります。気象の研究をする方には必須かもしれませんが(台風の進路や渦巻き等と関係)。もう一度基本から学び直してみましょう。
    
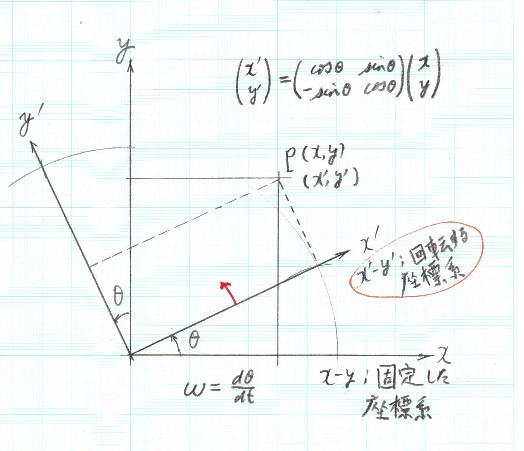
まずは、座標軸の回転です。座標(x,y)を角度θ回転して座標(x',y')に変換します。この準備ができたら、これを2回時間で微分します。丁寧にやらないと結構面倒ですね。
一回目の微分はいいとして、2回目はかなりゴチャゴチャして計算が大変です。後でマトリックス表示のまま微分して計算した結果も載せました。関数の積の微分ですね。
     まず1回目の微分。sinθ、cosθを微分したら、cosθ、－sinθに加えて、dθ／dtが出てくることに気をつけて下さい。2回微分したらd²θ／dt²が出てきますが等速円運動ではこれは零です。最終的に右辺もx'とy'を使って表せればいいのですが。

    
力学も面白い
ここで計算結果を整理して式を簡単にしていきます。回転している効果は速度、加速度の計算で出てきます。ここであなたが回転している座標系の上にいて、回転していることを知らなかったとしてみましょう。速度、加速度は単純に位置の座標変換と同じ形で変換されます。その結果あなたには見かけの力（余分な加速度）が生じることになります。
    
これが遠心力とコリオリの力です。以下同じ計算をマトリックス表示のままで行ってみました。この方が明らかに計算ミスは防げそうでしょう。

    
    
    
     更に一歩進めて、行列の形のまま計算できないものでしょうか。

力学も面白い

ロケットは何故飛ぶのか

ロケットは、宇宙開発には欠かせない道具です。翼もプロペラも無いのにどうして空を飛ぶのでしょう。この原理を最初に考えたのは、ロシアのツォルコフスキーという人です。原理は、ニュートン力学だけで説明できます。
ロケットは、空気のない宇宙空間を飛ぶことが出来ます。ロケットは、燃料（酸化剤を含む）を積んでそれ使いながら飛んで行くので、その総重量はだんだん軽くなって行きます。
でも、ロケットが普通の乗り物と異なるのは、初めから宇宙空間を飛ぶように考えられていることです。自動車なら燃料が無くなればそこで止まってしまいます。地面の摩擦や空気の抵抗があるからです。宇宙空間ではロケットはそのまま直線運動を続けます。等速直線運動と言うのでしたね。その時の速度は最終速度といいます。
でも、ここで言う速度とは地球に対しての速度です。宇宙では総ての物体がものすごい速度で互いに動いていて、絶対的な速さや位置は決めれないのでした。時間についてもあやふやになります。ニュートンに代わって、アインシュタインに登場願わないといけません。だから、ロケットは、燃料が無くなった途端に停止したとも考えれる訳(ロケットを基準にすれば)です。チョット不思議な感じがしますが。だから、思考の上でも、ロケットを学ぶことは宇宙へ飛び出すための第一歩となるでしょう。

まずは、ロケットの推進原理を簡単なモデルで考えましょう。
図のようなロケットが、宇宙空間を飛んでいます。ロケットの速度を v としましょう。この速度は観測者の位置（地上？？）を基準にしてます。ロケットからのガスの噴出速度はu(一定;ロケットに対して)です。
ロケットの質量をMとすると、M(t)は時間的に変化します。燃料を使うのでだんだん軽くなって行きます。積んでいる燃料を m とすると m(t) もどんどん減っていきます。この時、ロケットは Mv の運動量（質量×速度）を持っています。これに燃料を燃焼させた噴出ガス（速度u）の反作用で運動量が付加されていくので速度は加速されて行きます。噴出ガスの速度 u は、ロケットに対する速度です。ある時間tに対して微小な時間を経過した t＋dt 秒後の運動量はどうなるのでしょうか。

質量は M(t＋dt)＝M＋dm。 m は減少していく量なので dm は負となります。－dmは排出されるガスの質量(質量そのものは負にならない)で、排出速度は u で、ガスのもつ運動量は(－dm)(v－u)。従って、t＋dt秒後の運動量は
(M＋dm) (v＋dv)－dm (v－u)＝(Mv＋Mdv＋vdm＋dvdm)－(vdm－udm)＝Mv＋Mdv＋udm …(1)
dvdmは微小量の積で省略。このロケットには、宇宙空間では外力は働かず、運動量は保存されます（運動量保存則）。初めの運動量がMvだったので、Mdv＋udm＝0…(2)が求める微分方程式。ここでM(t)＝M₀－m
の関係があります。M₀＝M(0)のこと。つまり、ロケットは最初の質量から使った燃料分だけ軽くなっています。
結局下の式が得られます。
     dv/u＝－dm/M→→dv/u＝－dm/(M₀－m)…(2)
これは、変数分離型の微分方程式で両辺を積分することで解が得られます。
∫dv/u＝－∫dm/(M₀－m)→v/u＝－log|M₀－m|＋C…(3)

【対数関数の積分】
対数関数のところの積分は、少し分かりにくいと思います。
∫（m／((M₀－m)dm　ということは、∫(dx／/(a－x))を求めれば良いことですね。y＝a－x　と置くと、－∫dy/y＝－log|y|＝－log|a－x|とできます。logの中は正の数でないとまずいので絶対値をつけている。∫dx/x=log｜x｜は公式として高校でもやるかも。(d/dx)(log・x)＝1/xの逆演算です。この説明でとりあえず納得して下さい。
ここで、Cは初期条件から決まる積分定数。初期条件としてt＝0で、v＝0、m＝0とすれば、
0＝－log|M－M₀|＋C　だから→C＝logM₀が得られます。
従って、　v＝u・log(M₀/(M₀－m))＝u・log(M₀/M) →∴　(M₀/M)＝exp(v/u)…(4)
燃料を総て使い終わった時の最終速度v_kを求めます。準備していた燃料はm(0)、最初のロケットの重さは、M(0）で、ロケットが空になった時は、M_k＝M₀－m(0)となります。M_kは本体質量のことです。だから、
最終速度；　v_k＝u・log(M₀／M_k)
所要燃料；　m(0)＝M_k{exp(v_k／u)－1}

実際のロケットの発射は、地上から打ち上げるので地球の引力や大きな空気抵抗を受けるので、上の式がそのまま適用できるのは、宇宙空間での宇宙基地からの打ち上げる場合でしょう。しかし、この場合に限っても、ある質量のロケットを打ち上げるのに、その時必要な最終速度、必要な燃料の関係が求められることは、宇宙へ飛び立つ計画を立てるための第一歩であることは言うまでもないでしょう。

ツォルコフスキー(1857～1935年)は、「宇宙旅行の父」とも言われるほど、宇宙旅行に情熱を注いだ人。下記は有名な言葉。
Планеста есть колыбель разума, но нельзя вечно жить в колыбели.
「地球は、人類のゆりかごである。しかし人類はゆりかごにいつまでもとどまっていないだろう。」
**планеста＝惑星、衛星、колыбель＝ゆりかご、 разум＝理性、分別、 вечный＝永久の、 жить＝住む
Planest is the cradle of the mind, but you can't live in a cradle forever. →Земля - колыбель человечества, но человечество не будет оставаться в колыбели вечно.
“地球是人类的摇篮，但人类不会永远留在摇篮里。”Dìqiú shì rénlèi de yáolán, dàn rénlèi bù huì yǒngyuǎn liú zài yáolán lǐ.”

力学も面白い

ロケット(2)

ロケットが飛ぶ原理、もう一度復習です。自分自身の重量が変わっていくことは、今まで高校で習った力学とは少し異なるのでやはり分かりくい。もう一度自分で造るつもりで具体的に考えて見ます。
ロケットの重さをR＝10kgとします。燃料をF＝90kgとします。 R と F は rocket と fuel の頭文字。重さというところは正確には質量と言います。普通ロケットは燃料の重さが大部分なのです。
あなたは観測者で静止しているとします。つまりあなたが座標系の原点。どこか無重力の宇宙の中のどこかです。
t=0 で、ロケットの全質量はM=R＋F＝10＋90＝100kgです。ロケットの質量も、速度vも時々刻々変わります。ロケットは後部からガスを速度uで噴出してます。どのようにこの速度を造るかはまた新たな技術が必要ですが、ここでは燃料が無くなるまで一定の排出速度を得られるものとします。でも、この排出速度 u (m/s) は、排出ガスとロケットの相対速度で、あなたの座標系では排出ガスの速度は v－u となっています。
ある任意の時間 t でのロケットの質量をM、その時の速度をv とすると、ロケットは Mv の運動量を持っていることになります。M＝R＋F、つまりロケットの質量はロケット本体の質量R(10kg)と燃料 F の和ですが、F は初め(t＝0)では 90kg で、その後燃料を使用するたびにどんどん減っていきます。でも宇宙空間の真空中では運動量は保存されて時間が経過しても変わりません。
そこで、微小な時間 dt だけ経過した t＋dt での運動量を考えます。
  　(M＋dF)(v＋dv)＋(－dF)(v－u) …(1)
ここでdFは燃料の変化ですが、燃料は時間とともに減っていくので明らかに負の値を取ります。(1)式を整理すると、
  　 Mv＋Mdv＋vdF＋dFdv－vdF＋udF＝Mv＋Mdv＋udF
dFdv　は微小量の積で省略できます。運動量の変化は力積に等しいとの法則がありますが、外から力が加わらなければ運動量は保存されます。従って、時刻 t での運動量と時刻 t＋dt での運動量は等しくなります。だから Mdv＋udF＝0 …(2)が求める運動の方程式(微分方程式)です。変化する量は燃料の残量 F とロケットの速度 V です。(2)を書き直すと、
  　 dv/u＝－dF/(R＋F) → ∫dv/u＝－∫dF/(R＋F) …(3)
となりますが、この形を変数分離型と言います。左辺は v だけ、右辺は F だけの関数になっているからです。だから両辺は各々積分できます。これを求めると、
  　 v/u＝－log（R＋F）＋C …(4)
C は初期条件を決めないと決まりません。t＝0で、v＝0、F＝F₀ (燃料満タン)とすれば、0＝－log（R＋F₀）＋Cとなり、C＝log(R＋F₀) …(5)、従って求める関係式は、
  　 v＝u・log{(R＋F₀)/(R＋F)} …(6)となるので、上で求めた結果と全く同じものが得られました。R＋F₀＝M₀、R＋F＝Mとすれば同じです。
  　 (R＋F₀)/(R＋F)＝exp(v/u) …(7)
燃料が無くなった時点（F=O）が最終速度 v_k です。ロケットはこれ以上加速されることはなく、最終速度で宇宙空間を等速直線運動をします。この時の速度は(6)式から、
   v_k＝u・log{(R＋F₀)/R} …(8)
またこのために必要な所要燃料は(7) から、R＋F₀＝R・exp(v/u) 、 F₀＝R(exp(v_k/u)－1) …(9)
  　最終速度；v_k＝u・log{(R＋F₀)/R}　…(a)
  　所要燃料；F₀＝R(exp(v_k/u)－1)　…(b)
最初の仮定で R＝10kg、F₀＝90kg　としました。ロケットからのガスの噴出速度はどの程度まで可能なのでしょう。仮に u＝1000m/sとすると、(R＋F₀)/R＝(10＋90)/10＝10 となり、(a)から v_k＝2,300 m/s　となります。 v_k/u＝2.3 、
一方、所要燃料は、F₀＝R(exp(v_k/u)－1)＝10×{exp(2.3)－1}＝90kgでつじつまはあってます。
では、この燃料はどのくらいの時間持つのでしょうか。ツォルコフスキーの公式では、時間の要素が含まれてないのです。ガスの排出速度が同じでも、大量のガスを吐き出せば早く最終速度に到達するし、ゆっくり吐き出せば時間はかかるけど結局は最終速度に到達できる。どちらの場合も燃料の消費量は同じということだ。

例えは、燃料として液体水素と液体酸素の組合せを考えて見る。
   　 2H₂＋O₂→2H₂O
この式は、4 kg の液体水素と32 kg の液体酸素が反応して　36 kg の気体の水が発生することを表している。燃料が90 kg ということは、上の質量の2.5倍。10 kg の水素と80 kg の酸素を準備すれば良いことになる。水は液体のものが水蒸気になると約800倍ぐらい体積が増えるとされるが、更に燃焼によって体積が大きくなることが想定される。
ロケットが爆発しないために機体の中では反応せずに出口のノズル付近まで燃料（水素）と酸化剤（酸素）を輸送し、そこで排出量をコントロールしながら燃焼を行うという技術が必要だ。

力学も面白い

地上から発射

ロケットが地上から鉛直上向きに発射されます。ロケットが単位時間にμkg/s の割合でガスを噴出しています。先ほど記号を使うと -dF＝μdt 単位時間に排出されるガスの質量。ロケットの運動量は Mv だから、微小時間 dt 経過後の運動量は、(M＋dM)(v＋dv)＋(μdt)(v－u)となりますが、今回は、重力による下向きの力(力積)が加わる。Fdt＝－Mg・dt
   (M＋dM)(v＋dv)＋(μdt)(v－u)－ Mv＝－Mg・dt…(1)
   (Mv＋Mdv＋vdM＋dMdv)＋(μdt)(v－u)－ Mv＝－Mg・dt
ここで、dM＝dF＝－μdt、つまり燃料を使った分だけ機体は軽くなる。また、M＝M₀－μt、dMdvは微小なので省略できる
   (M₀－μt)dv＋v(－μdt)＋(μdt)(v－u)＝－(M₀－μt)g・dt
、整理すると dv{(M₀－μt)}＋dt{－μu＋(M₀－μt)g}＝0
   dv/dt＝{μu-(M₀－μt)g}／(M₀－μt)
   ∴　dv/dt＝－g＋μu／(M₀－μt)
これを積分する。右辺の積分は∫dt／(a－bt)＝I の形。a－bt＝x と置くと、dt＝－dx/bとなり、 I＝(－1/b)∫dx/x＝(－1/b)log|x|→μu(－1/μ)log|(M₀－μt)| (∵a＝M₀、b＝μ)
従って、v＝－gt－u・log|M₀－μt|＋C
t＝0の時、v＝0であるとすると、0＝－0－ulog|M₀|＋C、　∴C＝μlog|(M₀| であるから
  　v＝－gt－u・log|M₀－μt|＋μlog|M₀|
  　 v＝－gt－u・log|1－μt／M₀|…(1)
t 秒後の高さを求めるには、(1)をもう一度積分したい。
J＝log|1－at|の形の関数を積分するのだが、どうすれば良いのでしょう。
J＝log x なら部分積分法と言うのがある。公式は∫fg'dx＝fg－∫f'gdx
f＝log x 、g＝x としてみると、
J＝∫log x dx＝x log x －∫(1/x)x dx ＝x log x －x ＋C とできる。1－at＝x (ただし a＝μ／M₀)と置いて見る。－adt＝dx、∫log|1－at|dt＝(－1/a)∫log|x|dx ＝(－1/a)(x log x －x ＋C)＝（－M₀／μ）｛(1－at)log (1－at)－(1－at)＋C｝
初期条件として、t＝0で　h＝0とする。h は地上からの高さで、速度 v を積分したものとする。(1)を積分すると、
  　 h ＝(－1/2)g t²－u・（－M₀／μ）｛(1－at)log (1－at)－(1－at)＋C｝＝0
と相当ややこしい形になる。でも第一項の(－1/2) t²は自由落下の場合だ。
t＝ 0 であるから、－u・（－M₀／μ）{log 1－1＋C}＝ 0 なので、C ＝1
  　 h ＝(－1/2)g t²＋u・（M₀／μ）｛(1－μt／M₀)log (1－μt／M₀)＋μt／M₀)｝＝0 …(2)　(∵ a＝μ／M₀)
これが、地上からロケットを打ち上げた時にどこまで高く上げれるかを求める式となる。

ここで、μ／M₀＝1/60 とすると、ロケットは毎秒ロケットの初めの総量の1/60相当の質量のガスを噴出していることになる。また、ガス速度 u を 2,000m/s として、上式に代入する。
  　 h ＝(－1/2) gt²＋2000×60｛(1－t/60)log(1－t/60)＋t/60}…(3)

  
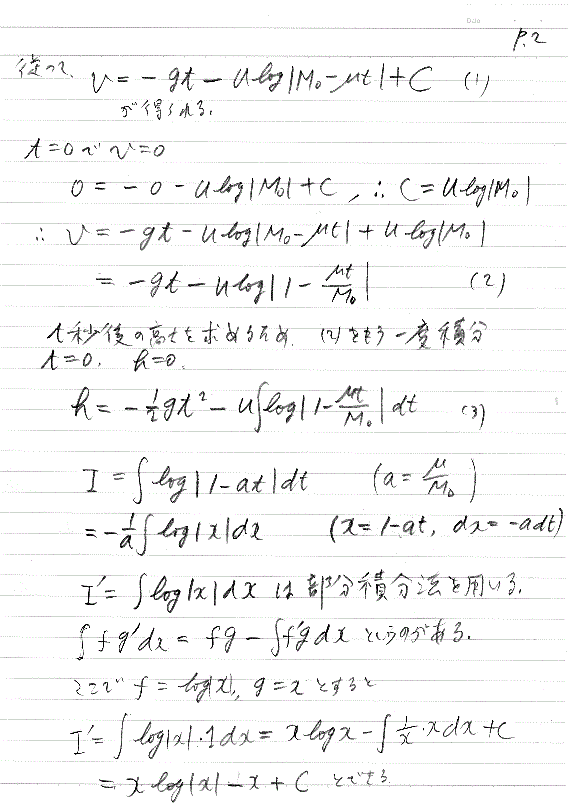
結構式はゴチャゴチャしている。
  
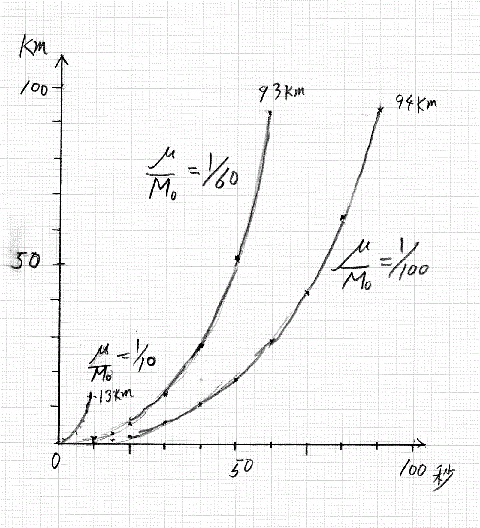
(3)式を元にExcelを用いて計算すると、ロケットの高さは、10秒後に1.27km、30秒後に14km、55秒後に70.3mと求めることが出来る。しかし、t=60秒ではエラーが出る。この時丁度燃料が蹴れたという仮定だ。これはlog の中が0になることからも納得できる。
μ／M₀＝1/60の仮定を考えて見ると、これは燃料を60秒で使い切ることだと分かる。高さ100ｋｍ弱までは上昇可能だ。でも、その後は計算できない。元々の方程式が燃料を噴出している条件で解析しているからだ。燃料を100秒で使い切るとしても結果には大差ない。最高点までの到達する時間が遅くなるだけ。燃料を10秒で使い切るとした結果かなり異なる。ほとんど上昇しないうちの燃料切れだ。
今回の計算は、ロケットを地上から打ち上げる際の問題だ。実際のロケットではこれに空気の摩擦を考慮しないといけない。摩擦は速度の2乗にほぼ比例すると言われるけどどうなのだろう。それとロケットが地上から遠く離れると重力加速度も小さくなる。地球の半径は6400kmだから、この例では g は一定でもいいかも知れないけど。それとこの例は燃料の量があまりにも少ない。
μ／M₀の値が1/60ということは燃料が1分(60秒)しか持たない前提だ。

燃料を使い終わった後のロケットの運動量の方程式は次のようになる。
   (M＋dM)(v＋dv)＋0＝Mv－Mgdt
ここで、dM＝0、Mはロケットの空の重量。だから、Mdv＝－Mgdtとなってしまう。つまり、dv/dt＝－g、ロケットに作用する加速度は地球の重力だけ。つまり自由落下です。宇宙に飛び出すためにはロケットのガス噴出速度を上げるか、継続時間を増やすしか方法がないようだ。
先の計算をμ／M₀＝1/600、u＝10000m/sで行って見た。初めは機体が重たいせいか上がる速度は遅いけど、最終的には高度2000 km 近くまで上がるようだ。10分経過すると燃料が無くなり自由落下するのか。ただここまで上がると重力の影響もだいぶ小さくなるはずだ。

力学も面白い

地球の引力

ニュートンが木からリンゴが落ちるのを見て万有引力を発見したと本気で信じ込んでいる人もおおいだろう。でも何故ニュートンがこんな研究に執念を燃やしたのかそれでは説明がつかない。ニュートンが解明したかったのは天体の運動だ。当時、ヨハネス・ケプラーの大きな発見があった。当時の人々は天体は神が作った世界なのでどの星々も同じようにきれいな円運動をしているものと信じていた。でも惑星の運動は例外だった。信心深いニュートンは何とか神の定めた美しい法則を発見したいと情熱を燃やしていたのでしょう。
ケプラーは師ティコ・ブラーエが残した膨大な観測記録から、太陽に対する火星の運動を推定し、以下のように定式化した。
① 第1法則(楕円軌道の法則)
  　…惑星は、太陽を焦点のひとつとする楕円軌道上を動く。
② 第2法則(面積速度一定の法則)
  　…惑星と太陽とを結ぶ線分が単位時間に描く面積（面積速度）は、一定である。
③ 第3法則(調和の法則)
  　…惑星の公転周期の2乗は、軌道長半径の3乗に比例する。

第一、第二法則の発見は1609年、第三法則は1619年に発表されました。
ニュートンは、1687年「プリンキピア(自然哲学の数学的諸原理）]の中で、万有引力の法則と運動方程式について述べ、古典力学（ニュートン力学）を創始。 これによって天体の運動を解明された。ケプラーの発見から68年後。機は熟していたということだろう。
以下は万有引力について
  　 F= G (M m)／r²
とても有名な公式ですね。二つの物体　M(kg)とm(kg)には相互に力F(N＝kgm/s²)が働き、その力は物体間の距離の2乗の反比例するというもの。
ニュートン力学では、物体の質量はその重心に集まっているものと見なしても良いことになってます。つまり天体での総ての物質は質点と見なすことが可能です。
地球の半径は約6400km と大きいので地上での運動では R＝6.4×10⁶m として一定とすることが出来ます。
つまり　重力加速度は　 g＝(GM/R²)として
g の値としてだいたい g＝9.8m/s²が使われています。つまり F ＝mg です。
なお、地球の質量 M と 万有引力定数 G としては、
  　M＝6 ×10²⁴kg    G ＝6.67259 ×10^-11 m³s^-2kg^-1
地上で建物を設計したり、飛行機を飛ばす時（せいぜい高度10000ｍ）はRは一定でもいいでしょうが、ロケットの場合はもっと高く飛ばすでしょう。この補正は
  　 g' ＝g (R/(R＋h))² とすれば良いことはすぐに分かると思います。地球の半径と同じだけ高く飛べは引力は1/4になります。半径の9倍高く上がれば引力は1/100。地球の引力の影響をほとんど受けなくなります。

力学も面白い

宇宙速度

宇宙速度（escape velocity,　Космическая скорость）とは、地表において物体にある初速度を与えたとして、衛星軌道などの「宇宙飛行」と言えるような軌道に乗せるために必要な速度のことである。特に地球および太陽に対して、第一宇宙速度・第二宇宙速度・第三宇宙速度と呼ばれている速度がある。他の星や星系（恒星、惑星、衛星等）に対しても同じように使える。なお、通常は重力のみを考慮し、空気抵抗・浮力等は加味しない。このようなことを考える学問を軌道力学と言うらしい。

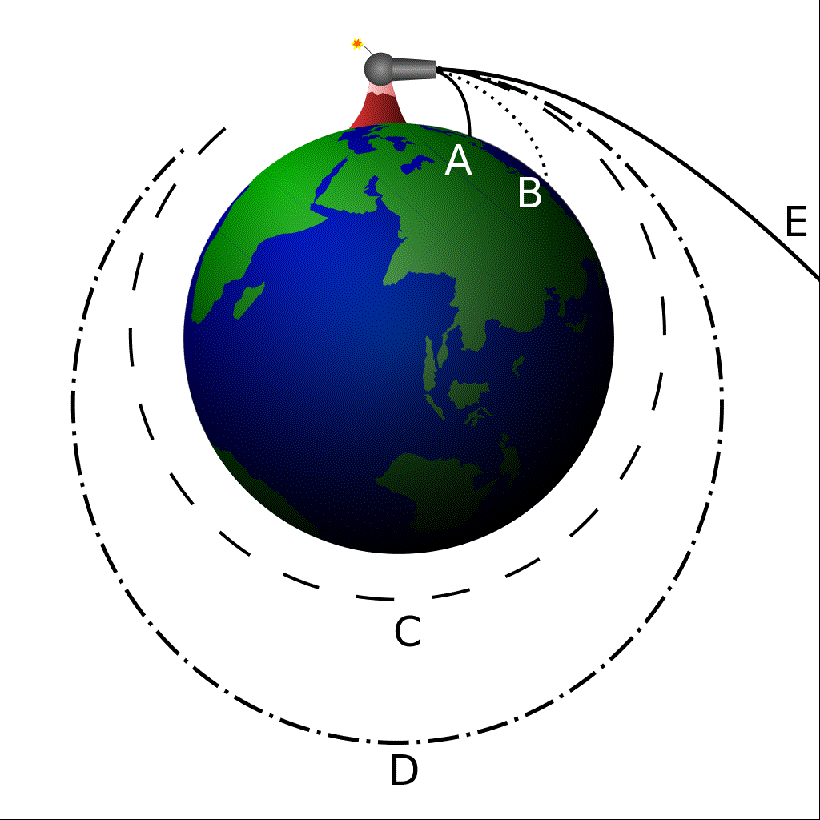まずは右図をご覧下さい。
A. 地表から水平に打ち出された砲弾は重力に引かれて地表に落下する (A)。
B. 射出速度を上げても第一宇宙速度未満ならいつかは地表に落下する (B)。
C. 第一宇宙速度で打ち出された場合は人工衛星となる (C)。
D. それ以上の速度では楕円を描き (D)、
E. 第二宇宙速度以上の場合は地球の重力を振り切る (E)。（ただし大気の抵抗による影響などは考慮していない）。

第一宇宙速度
第一宇宙速度とは、地球において、その高度を海抜ゼロ（海面もしくは地表すれすれ）とした（仮想上の）円軌道で。速度約 7.9 km/s (= 28,400 km/h) となった場合。地表において、ある物体にある初速度を与えた場合、速度がこれ未満の場合はどのように打ち出したとしても弾道飛行 (sub-orbital flight) の後に地表に戻る。逆に、これを越えて (super-orbital) （第二宇宙速度未満で）水平に打ち出した場合、その地点を近地点とする楕円軌道に投入される。
第一宇宙速度は、円運動を続けようとする物体の遠心力と引力との釣り合いから、
(mv²/R)＝GmM/R²。　これよりｖ＝√GN/R＝7.91 km/s

第二宇宙速度（地球脱出速度）
第二宇宙速度とは、地球の重力を振り切るために必要な、地表における初速度である。約 11.2 km/s（40,300 km/h）。第一宇宙速度の √2 倍である。地球から打ち上げる宇宙機を太陽を回る人工惑星にするためには第二宇宙速度が必要である。地球の重力圏を脱出するという意味で地球脱出速度とも呼ばれる。地球以外の任意の星についてや、あるいは「ある高度における脱出速度」といったものも考えられる。
地球からの無限遠点を基準として、質量 m の物体の地球表面における地球重力によって生じる位置エネルギーは、U=－∫_∞^R(－GMm/r²)dr＝－GMｍ/R。この負のエネルギーを打消す運動エネルギーを与えれば、地球の重力圏から脱出できる。
  　(1/2)mv²－GMm/R＝0、これより v=√（2GM/R）＝(√2)v₁＝11.2 km/s

第三宇宙速度
第三宇宙速度とは、第二宇宙速度と同様の考え方で地球軌道・地表においてある初速度を与えたとして、地球さらには太陽の重力を振り切るために必要な速度で、約 16.7 km/s (60,100 km/h) である。太陽の質量、地球の質量、太陽と地球の距離、地球の半径、万有引力定数から求めることができる。現実的には地球の公転速度を利用する側に飛び出すか逆かでΔvとしては違ってくる。また、惑星探査機などではスイングバイを利用して加速するものも多い。

ロケットは真上に打ち上げられるものと思っていたが、地平線に水平に打ち上げられることもあるんだ。しかし地上で真上に打ち上げられたと思っているロケットも案外そうではないかも。地球上では地球の自転に伴う遠心力やコリオリの力も無視できない。多くの宇宙へ向かうロケットが赤道に近い所で発射されているようだし。

力学も面白い

中心力による運動

ケプラーは師のティコ・ブラーエが観測した膨大な資料を整理研究して、ケプラーの 3 法則を発見したとされる。
① 第1法則(楕円軌道の法則)
  　…惑星は、太陽を焦点のひとつとする楕円軌道上を動く。
② 第2法則(面積速度一定の法則)
  　…惑星と太陽とを結ぶ線分が単位時間に描く面積速度は、一定。
③ 第3法則(調和の法則)
  　…惑星の公転周期の2乗は、軌道長半径の3乗に比例。
当時は、占星術(天体観測)と錬金術(化学)が流行っていた時代。著名なティコ・ブラーエが観測した事実は覆せないので、何か神の意思を読み解くための理論を世の中も求めていたらしい。
火星を始め惑星は、太陽を中心にして平面運動をする。これは他の惑星も同じ。万有引力の理論からは太陽の方も惑星に引っ張られて多少動いているのですが、まあ、質量に差があるので太陽の動きは無視しましょう。
本当は、ケプラーの法則からどのようにして万有引力が導かれたかを知ることの方が興味はあるのでしょうが、ここでは万有引力を仮定してケプラーの 3 法則を導いてみましょう。
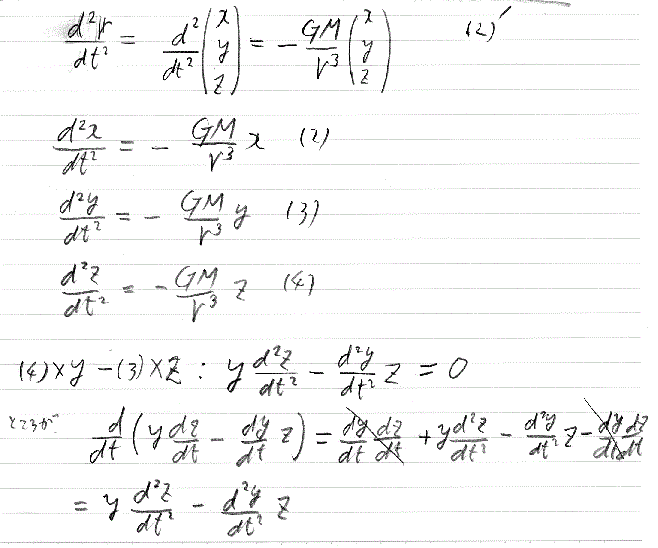ここで言う中心力とは、惑星に働く力が何時も太陽の方向(中心)に向いている運動をいう。万有引力の法則は次の通りでした。
   　F＝－(GMm/r³)r
ここで注意すべきは、距離 r が2乗ではなく3乗となっていること。これは式がベクトルとして表示してあるためで、r/rはr(動径)方向の単位ベクトルです。ベクトルは太字で表わすか文字の上に矢印をつけるのが習慣ですが、htmlの表示ではあまり分かりやす表時出来ません。手書きの物の方が見やすいかも。
ここで、Gは万有引力定数、M は太陽の質量、m は惑星の質量、r は太陽と惑星の距離（動径）です。太陽の位置をS(0,0,0)、 惑星の位置をP(x,y,z)、つまりr＝(x,y,z)
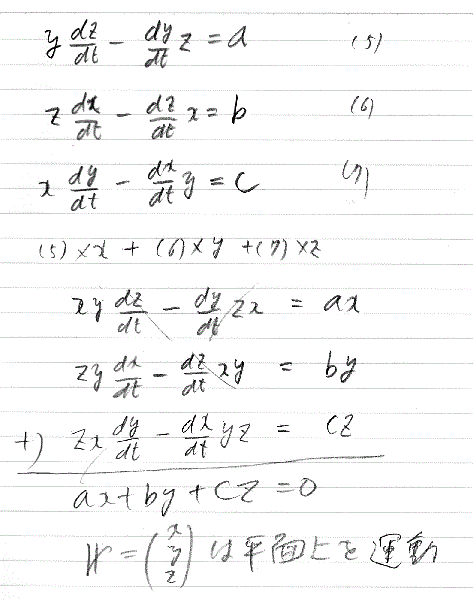ニュートンによる運動の方程式（質量×加速度＝力）をx、y、z成分に分けて記したのが、(2)、(3)、(4)です。この式を見れば、右辺にある力の項を消すことが出来ることが分かります。例えば、(4)×y －(3)×z とすれば、
   　yd² z /dt²－d² y /dt²z＝0
実はこの式は、ydz /dt－dy /dt・z をtで微分(d/dt)したもの。微分した結果が零のなので元の式は定数( a )です。同じように定数b、cを使って、(5)、(6)、(7)式を得ます。
(5)×x＋(6)×y＋(7)×zを作ってみます。何と微分の項は消えて、ax＋by＋cz＝0 となってしまいます。これは良く知られている原点を通る3次元空間上の平面の式です。つまり点P(x、y、z)で示される惑星は太陽のある原点を通る平面上を運動していることをしてしているのです。
この結論は大きな示唆を我々に与えてくれます。太陽を回る惑星は皆一つの大きな平面上を運動しています。銀河が平たい円盤状の形をしている理由もこれで分かります。将来人類が太陽系内を飛び回る時、ロケットの運動もこのようになるわけです。
運動が平面内で行われると、運動の考察は飛躍的に簡単になります。2次元の考察で済むからです。座標軸がxとyの普通の座標で考えれます（z 軸が不要に）。
【面積速度】
惑星P が中心力を受けて太陽Sの周りを回っています。この時面積速度は、動径が描く微小な面積 △S ＝(1/2)r²△θ
の極限（△θ→0）として表されます。
   　dS/dθ＝lim△S/△θ＝(1/2) r²    　面積速度 dS/dt＝dS/dθ・dθ/dt＝(1/2) r²dθ/dt
また、平面運動では先ほどの計算結果から、 x (dy/dt)－y (dx/dt)＝h (h は定数で先ほどはc)
ここで座標を極座標に変換します。x＝r cosθ、y＝r sinθ
  　(dx/dt)＝(dr/dt) cosθ－r (dθ/dt) sinθ、(dy/dt)＝(dr/dt) sinθ＋r (dθ/dt) cosθ となるので
   　 x (dy/dt)－y (dx/dt)＝r cosθ {(dr/dt) sinθ＋r (dθ/dt) cosθ}－r sinθ{ (dr/dt) cosθ－r (dθ/dt) sinθ}
      　＝(dr/dt){rcosθsinθ－r sinθcosθ}＋(dθ/dt){r²cos²θ＋r² sin²θ}
      　＝r²(dθ/dt) ＝ h
r²(dθ/dt) ＝ h が得られ、面積速度は
      　dS/dt＝(1/2) r² dθ/dt＝ h/2
結論として、距離の2乗に反比例する力（ニュートンの万有引力）の場における運動の面積速度は一定（ケプラーの第二法則）となります。

力学も面白い

中心力による運動(2)

中心力による運動は、万有引力に限らず、平面運動を行い、面積速度が一定になるらしい。力の中心を原点に取り、原点から仏体 P に向かうベクトルを r とする。中心力は一般的に、F＝K rと表わせる。運動方程式は m d²r / dt²＝Kr となる。
x、y、z の成分表示をすれば、 d² x / dt²＝K x /m　、 d² y / dt²＝K y /m　、 d² z / dt²＝K z /m　
とできる。前に行ったように、力の項を消去すれば、(第3式に y をかけたものから第2式に z を掛けたものを引く)
    y d² z /d t²－d² y / d t² z＝0 →y d z/d t－(d y / d t) z＝a
同様にして 3 つの式が得られる。y dz / dt － d y / d t z ＝a(一定) 、z dx / dt － d z / d t x ＝b(一定) 、x dy / dt － d x / d t y ＝c(一定)
この第1式、第2式、第3式にそれぞれx、y、z をかけて加えると、ax＋b＋cz＝0　となって、平面運動を行うことが分かる。
万有引力の場合は、K＝GMm / r³ であったが、一般の中心力でも平面運動になる。
この平面をx-y 平面をすれば、x dy / dt － d x / d t y ＝h とでき、極座標を使って、
    d S / dt ＝ (1/2) r² dθ/ dt ＝h/2 となる。
中心力の場では面積速度が一定になる。逆に面積速度が一定なら中心力になることも以下のように示せます。 d S / dt ＝ (1/2) r² dθ/ dt ＝h/2 ならば、
    r² dθ/ dt ＝x dy / dt － d x / d t y ＝h
この両辺を t で微分すると、x dy² / dt² － d x² / d t²・ y ＝0　なので、x / y ＝ (d x²) / d t²)／( d　y² / dt²)　
動径の向きと力(加速度)の向きが、F_x / F_y ＝ x / y　のように等しくなり、これが中心力になっていることが分かります。

力学も面白い

惑星の軌道(ケプラーの第1法則)

いよいよ惑星に軌道に挑戦します。天体の運動はほとんどが楕円運動らしい。けれども日常生活で楕円を考えねばならいケースはほとんどない。一体どんな式が飛び出すのか。
まずは、惑星の運動方程式。
    m d²x / d t²＝－(G M m/r³) x …(1)
    m d²y / d t²＝－(G M m/r³) y …(2)
すなわち、
   　d²x / d t²＝－(G M /r³) x …(3)
   　d²y / d t²＝－(G M /r³) y …(4)
G M ＝ k とおいて、
   　d²x / d t²＝－k x /r³ …(5)    　d²y / d t²＝－k y /r³ …(6)
一方、面積速度は、d S / dt ＝(1/2) r² dθ / dt ＝ (1/2) h …(7)であった。
すなわち、dθ / dt ＝ h / r²、 1/ r ＝ u とおくと、dθ / dt ＝ h u²
u は　距離 r の逆数だ。また、x ＝ r cos θ＝ (1/u) cosθ とおくと、
   　dx / dt ＝ (dx /dθ)(dθ/ dt) ＝　h u² d/dθ((1/u)cos θ)
     　＝－h u² {－(1/u²)(d u / dθ)cos θ －(1/u)sinθ}
     　＝－h ((du / dθ)cosθ＋u sin θ)
従って、dx² / d t²＝d/dt(dx / dt)　＝　d/dθ(dx/dt)(dθ/ dt)
     　＝ h u² {－h [(d u /dθ)cos θ＋u sinθ]}
     　＝ －h u²{(d² u / dθ²)cosθ　－ (d u/dθ)sinθ　＋ (d u/dθ)sinθ ＋u cosθ}
     　＝－h u²(d² u / dθ² ＋　u )cosθ
これを上の(3)式に代入し、右辺のxとrをuとθであらわすと、
     　－h u²(d² u / dθ² ＋　u )cosθ＝ －k u² cosθ
これを整理して、　 d² u / dθ² ＋　u ＝ k / h²
ようやく、動径 r (の逆数 u＝1/r)と角度θに関する微分方程式が求まったのでこれを解いてみよう。まずここで、 w ＝u－ k /h²　と変数変換すると、
     　 d² w / dθ² ＋　w ＝0
これは良く知られた単振動の方程式。その解は、 w＝A cos(θ－α) 、A とαは初期条件から決めなければいけない。
     　 u ＝A cos(θ－α)＋ k /h²
      　＝(k/h²)　{ 1＋(Ah²/ k)cos(θ－α) }
更に、Ah²/ k＝e、h² / k ＝ p とおく。
     　(1/r)＝(1/p)(1＋e cos(θ－α) )
     　 r ＝　p /( 1＋e cos(θ－α))
これが求める楕円の方程式。極座標表示ではこうなるのです。

力学も面白い

ケプラーの第3法則

「ケプラーの第3法則は惑星の公転周期の2乗は楕円の長軸の3乗に比例する。」というものでした。楕円軌道の周期を T とする。面積速度は一定で dS/dt ＝ h/2 なので、1周期の間に動径の描く面積は、　∫₀^T dS/dt dt＝ (h/2) T、これが楕円の面積になります。
つまり、楕円の半長軸を a 、半短軸を b とすると、(h/2) T ＝πab、つまりT ＝2πab / h となります。
ところで、長軸と短軸の間には b ＝ a√(1－e²) の関係があります。
   　T＝2πa √( 1－e²) 、 T²＝4π²a⁴( 1－e²) / h² …(1)
ところで長軸の長さは 2a ＝p / (1－e)－p / (1＋e)（§ 惑星の軌道(ケプラーの第1法則)のB－図参照）
すなわち、p＝( 1－e²) a 、これを(1)に代入すると、
T²＝4π²a³ / h² ＝ 4π²a³ / k   　(∵ h²/k ＝ p としている)
これより、公転周期の2乗は、軌道の長半径の3乗に比例（T² ∝a³）することが言えた。

力学も面白い

静水圧とは

　アリストテレスは、力が物体に作用すると物体は動き(運動し)、力が働かなければ物は動かないと考えていた。コップに水を入れておいておけば、水は力が働いていないので動かない。しかし、コップは水が入ったため明らかに重くなっており、それが置いてある机により多くの圧力を与えるだろう。あなたが机を下向きに押せば、力が必要ですが机は動きません。また、あなたがいかに力持ちでもあなたの体重よりも大きな力で下向きに押すことは不可能です。ここで、作用反作用の法則を思い出してください。机が動かないということは、机から上向きの力が働いているのでしたね。動かないということは、力が働いていないのではなく、働いている力が釣り合っているためと分かることは大きな進歩です。
　では、圧力とは何でしょう。簡単に言えば単位面積当たりの力です。あなたが面積Sの板の上に乗り、あなたの体重がM(kg)とすると、その時の圧力P(N／m²)は、
P＝M g／S　【N／m²】、    gは重力加速度で地上では、9.8m/s²、体重も正確には質量と言わねばなりません。ところがあなたが乗った板には本当に均等な圧力がかかっていたとは言えません。上のPは、平均の圧力です。実際には板の端と真ん中では異なる圧力でしょう。
　ちょっと話がそれますが、土木や建築の分野では、出来上がったコンクリートの強度を確認するために、現物と同じ条件で試験練(ねり)として拵(こしら)えた円柱の供試体を何本も造り、これを機械的に潰してどこまで耐えられるか試験します。この試験体をつくる円柱の大きさ等の仕様はキチンと決まっていて、これ以外は認められません。所要のコンクリート強度を確保するためには結構色々な条件を考慮する必要があるのです。強度というのはコンクリートの内部に発生する圧力に対する耐久力です。コンクリートの年齢(打設してからの時間経過)、配合(水、砂、砂利、セメントの量と割合)、温度等色々考慮する必要がありますが、円柱の大きさが決まっている最大の理由は、コンクリートの場合、内部の圧力の分布は均一にはならないためです。供試体が大きい方が耐久力があるようです。
　この点、水(流体)を対象にすると圧力はずっと簡単になります。水圧は、流体の中に仮想の面を考えると面がどちらに向いていても面に垂直な成分しかありません。上で述べたコンクリートのように面の向きで圧力の値が異なったり、面に平行な成分が発生するものを応力と称しています。詳しくは、材料力学等の分野を学ぶ必要があります。
【水中の一点に作用する水圧は、その方向にかかわらず強さが等しい】
左図に示すように、一辺が鉛直な三角形△ABCの単位幅のの仮想三角柱が水中にあるとする。ちょうどプリズムのような形。作用する力は下向きの重力だけです。二次元で考えて紙の厚さ方向は単位幅としています。
水平方向のに働く力は辺ABに働く圧力の合計と辺BCに働く圧力の合計の水平法の分力が釣り合います。鉛直方向は、辺ACに働く圧力の合計とプリズムの重さWを加えたものが辺BCに働く圧力の合計の鉛直上向きの力と釣りあっていないといけません。
ところが仮想のプリズムは大きさも任意なのでこれをうんと小さくして極限として0とすると、結局プリズムのどの面に働く圧力は同じ、つまりp₁＝p₂＝p₃となることが分かります。圧力は小文字で表わしています。
でも、チョット騙された気がする人いませんか。仮想三角柱をどんどん小さくすればその重さも小さくなるけど、各辺に作用する力だって小さくなってしまうんじゃない。どうしてWだけ省略できるんだ。良く絵を見て下さい。各辺に働く力は辺の長さに比例するでしょう。でも重さはプリズムの面積（長さの2乗）に否定するので、小さくなる速さがずっと速いから無視できるのです。

結局水中の圧力は、深さが一定ならどの方向でも一定になります。金魚の水槽などに水を張って静かにおいておくと水は全く動かなくなるでしょう。インクを静かにスポイトで入れてもほとんど動かないですね。圧力に差があれば水は圧力の高い方から低い方に必ず動きます。材料が固体(剛体ではない)ではこうならず、応力テンソルという物理量が必要になります。物理の世界では水は理論化しやすい優等生なのです。




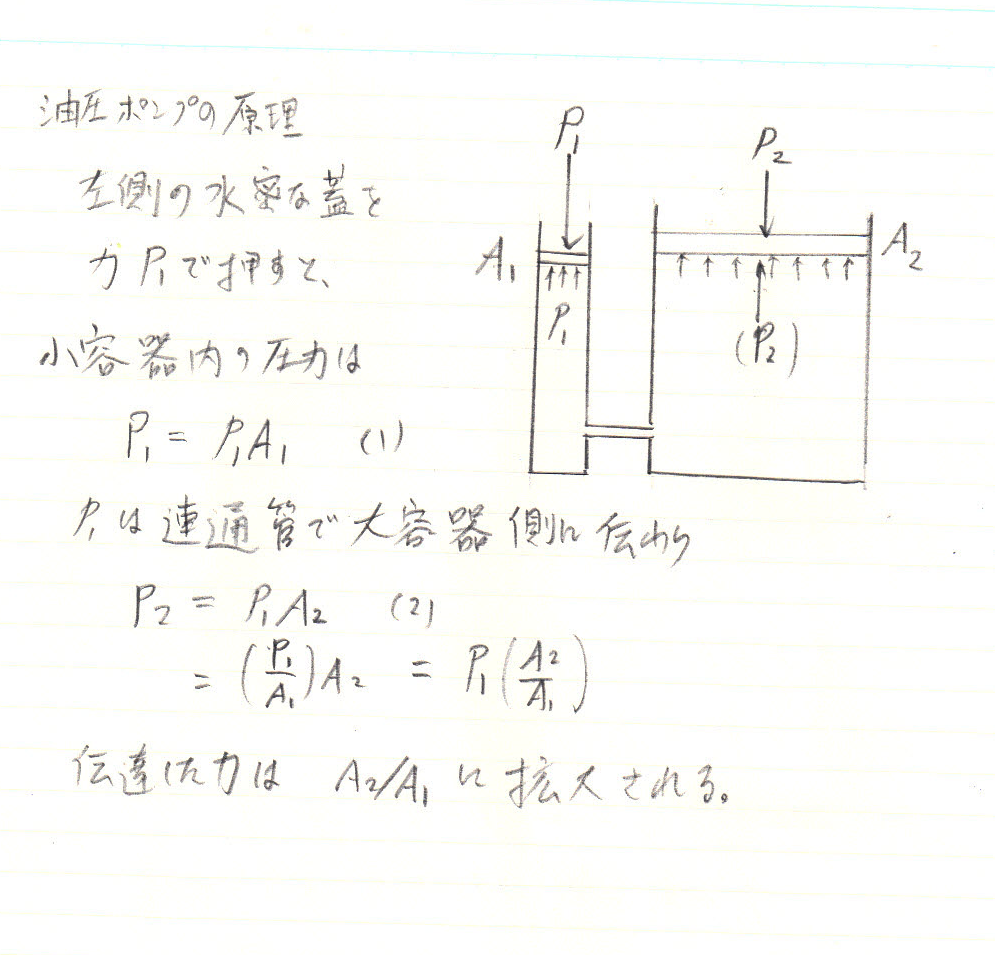結局静水圧とは深さだけの問題ですね。次に示すのはパスカルの原理とも言われているもので、「密閉容器中の流体は、その容器の形に関係なく、ある一点に受けた単位面積当りの圧力をそのままの強さで、流体の他のすべての部分に伝える。」 というもの。左側の小さな面積A₁に思い切り大きな圧力をかけるとその圧力がそのまま大面積A₂に伝えられる仕組みです。建設機械等に使われる油圧の原理もこれです。

力学も面白い

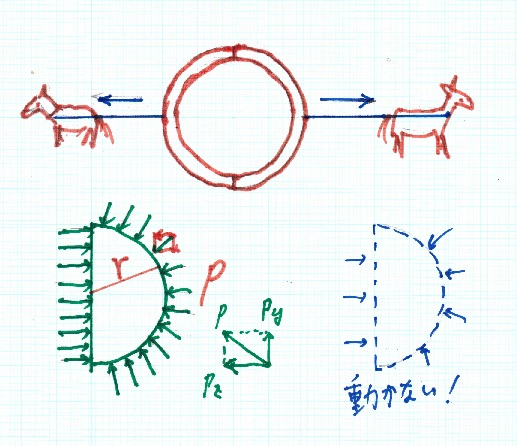
マグデブルクの半球

大気圧の力を示す歴史上有名な実験。17世紀のドイツでオットー・フォン・ゲーリケという人が行なった。
半球は、中が中空の2つの金属製の半球で、縦に2つに割ったメロンをイメージ。すきまなく接合するように作られ、この2つを合わせ、ゲーリケ自らが発明した真空ポンプで中の空気を抜く。間には濡らした動物の皮をパッキンとして使用。こうすると半球はぴったりくっつき、どんなに引っ張っても外れない。外側の大気圧によるものである。
ゲーリケはこの実験を公開実験で行った。最初のものは1654年5月8日、レーゲンスブルクの帝国議事堂前において、神聖ローマ皇帝フェルディナント3世の御前で行われた。このとき、16頭の馬（両側から2頭立ての馬が各4対）が双方から引っ張り、やっと半球は外れた。この実験により、デカルトが否定した真空の存在を証明した。「マクデブルクの半球」の呼び名は、当時ゲーリケがマクデブルク市長であったことに由来するそうです。1970年代にNHKの『ハテナゲーム』で再現されたそうです。

マグデブルグの半球
   この実験を思考実験で確かめてみましょう。半球に作用する大気圧pは一様均等に作用しています。この合力を求めましょう。ところがpは、半球の上で方向が各々異なります。そこで、水の中に仮想の半球を考えます。この仮想に半球は静止した水の中にあるので当然動きません。だから右側の圧力の合計は、左側の半円の上に作用する圧力の合計です。また、圧力pを鉛直方向と水平方向に分けて、鉛直方向は上下方向が互いにキャンセルされて、水平方向だけ残り、上と同じことが言えます。本当は紙面を突き抜けるx方向も考える必要がありますが。上の説明ならどんな形でも適用可能です。
大気の圧力は、水に置き換えると、およそ10ｍの水柱に相当します。だから、
       p＝1000kgf/m³×10m＝10000kgf/m²
半球の半径rを30cmとすると、面積はa＝πr²＝0.2827m²
従って、馬が引張らなければならない力Tは、
      T＝p×a＝2827kgf＝2.83ton、やはり相当大きな力だ。1kgf＝9.8N(ニュートン)ですからT＝27700Nの方が正式か。
大気圧は、p＝98000N/m²＝980hPaとなるが、実際にはだいたい1013.25 hPaとされている。だから10m水柱という大雑把な見積は3%程度少な目のようだ。
ところで、この検討では、半球(鉄製らしい)の肉厚は考慮されていない。中が中空でなくて本当に密実な半球でも接着面を平滑にして水でも入れて空気が入らないようにして密着すると半球は離れなくなる。接着面の水が乾かないと簡単には取れないはずだ。

力学も面白い

水理学再入門

　水理学とは、流体力学の中でも水だけを対象にする。気体には圧縮膨張や熱的変化等力学においても色々と考慮すべき事項が多い。その点水は非圧縮で、密度が一定。取りあえずモデル化しやすい。水理という呼び方は、どちらかと言うと土木や地球物理の分野で、川の流れや海の波、上下水道などの開渠や暗渠などでの実用的な流れの解析を中心に発達してきた。私自身、若いころ研究所で色々勉強したのですが、最近は使うことがなくてすっかり忘れていました。再度学び直して見ようとの趣旨から勉強を始めたので宜しくお付き合いの程を。

目次 　　

静水圧とは	マグデブルクの半球	一次元流れ	Eulerの運動方程式	流れ関数	速度ポテンシャル
時間に関する微分

静水圧とは

　アリストテレスは、力が物体に作用すると物体は動き(運動し)、力が働かなければ物は動かないと考えていた。コップに水を入れておいておけば、水は力が働いていないので動かない。しかし、コップは水が入ったため明らかに重くなっており、それが置いてある机により多くの圧力を与えるだろう。あなたが机を下向きに押せば、力が必要ですが机は動きません。また、あなたがいかに力持ちでもあなたの体重よりも大きな力で下向きに押すことは不可能です。ここで、作用反作用の法則を思い出してください。机が動かないということは、机から上向きの力が働いているのでしたね。動かないということは、力が働いていないのではなく、働いている力が釣り合っているためと分かることは大きな進歩です。
　では、圧力とは何でしょう。簡単に言えば単位面積当たりの力です。あなたが面積Sの板の上に乗り、あなたの体重がM(kg)とすると、その時の圧力P(N／m²)は、
P＝Mg/S　【N／m²】、
gは重力加速度で地上では、9.8m/s²、体重は正確には質量と言わねばなりません。ところがあなたが乗った板には本当に均等な圧力がかかっていたとは言えません。上のPは、平均の圧力です。実際には板の端と真ん中では異なる圧力でしょう。
　ちょっと話がそれますが、土木や建築の分野では、出来上がったコンクリートの強度を確認するために、現物と同じ条件で試験練(ねり)として拵(こしら)えた円柱の供試体を何本も造り、これを機械的に潰してどこまで耐えられるか試験します。この試験体をつくる円柱の大きさ等の仕様はキチンと決まっていて、これ以外は認められません。所要のコンクリート強度を確保するためには結構色々な条件を考慮する必要があるのです。強度というのはコンクリートの内部に発生する圧力に対する耐久力です。コンクリートの年齢(打設してからの時間経過)、配合(水、砂、砂利、セメントの量と割合)、温度等色々考慮する必要がありますが、円柱の大きさが決まっている最大の理由は、コンクリートの場合、内部の圧力の分布は均一にはならないためです。供試体が大きい方が耐久力があるようです。
　この点、水(流体)を対象にすると圧力はずっと簡単になります。水圧は、流体の中に仮想の面を考えると面がどちらに向いていても面に垂直な成分しかありません。上で述べたコンクリートのように面の向きで圧力の値が異なったり、面に平行な成分が発生するものを応力と称しています。詳しくは、材料力学等の分野を学ぶ必要があります。
【水中の一点に作用する水圧は、その方向にかかわらず強さが等しい】
図-1 図－2
図1に示すように、一辺が鉛直な三角形の単位長さの仮想三角柱が水中にあるとする。鉛直としたのは、この三角柱に作用する力は下向きの重力だけとしているから。
結局水中の圧力は、深さが一定ならどの方向でも一定になります。材料が固体(剛体ではない)ではこうならず、応力テンソルという物理量が必要になります。
図－2
結局静水圧とは深さだけの問題ですね。次に示すのはパスカルの原理とも言われているもので、「密閉容器中の流体は、その容器の形に関係なく、ある一点に受けた単位面積当りの圧力をそのままの強さで、流体の他のすべての部分に伝える。」 というもの。建設機械等に使われる油圧の原理もこれですね。
図-3

力学も面白い

マグデブルクの半球

大気圧の力を示す歴史上有名な実験です。17世紀のドイツでオットー・フォン・ゲーリケが行ないました。
半球は、中が中空の2つの金属製の半球で、縦に2つに割ったメロンをイメージ。すきまなく接合するように作られ、この2つを合わせ、ゲーリケ自らが発明した真空ポンプで中の空気を抜く。間には濡らした動物の皮をパッキンとして使用。こうすると半球はぴったりくっつき、どんなに引っ張っても外れない。外側の大気圧によるものである。
ゲーリケはこの実験を公開実験で行った。最初のものは1654年5月8日、レーゲンスブルクの帝国議事堂前において、神聖ローマ皇帝フェルディナント3世の御前で行われた。このとき、16頭の馬（両側から2頭立ての馬が各4対）が双方から引っ張り、やっと半球は外れた。この実験により、デカルトが否定した真空の存在を証明した。「マクデブルクの半球」の呼び名は、当時ゲーリケがマクデブルク市長であったことに由来するそうです。1970年代にNHKの『ハテナゲーム』で再現されたそうです。

マグデブルグの半球
   この実験を思考実験で確かめてみましょう。半球に作用する大気圧pは一様均等に作用しています。この合力を求めましょう。ところがpは、半球の上で方向が各々異なります。そこで、水の中に仮想の半球を考えます。この仮想に半球は静止した水の中にあるので当然動きません。だから右側の圧力の合計は、左側の半円の上に作用する圧力の合計です。また、圧力pを鉛直方向と水平方向に分けて、鉛直方向は上下方向が互いにキャンセルされて、水平方向だけ残り、上と同じことが言えます。本当は紙面を突き抜けるx方向も考える必要がありますが。上の説明ならどんな形でも適用可能です。
大気の圧力は、水に置き換えると、およそ10ｍの水柱に相当します。だから、
       p＝1000kgf/m³×10m＝10000kgf/m²
半球の半径rを30cmとすると、面積はa＝πr²＝0.2827m²
従って、馬が引張らなければならない力Tは、
      T＝p×a＝2827kgf＝2.83ton、やはり相当大きな力だ。1kgf＝9.8N(ニュートン)ですからT＝27700Nの方が正式か。
大気圧は、p＝98000N/m²＝980hPaとなるが、実際にはだいたい1013.25 hPaとされている。だから10m水柱という大雑把な見積は3%程度少な目のようだ。
ところで、この検討では、半球(鉄製らしい)の肉厚は考慮されていない。中が中空でなくて本当に密実な半球でも接着面を平滑にして水でも入れて空気が入らないようにして密着すると半球は離れなくなる。接着面の水が乾かないと簡単には取れないはずだ。

力学も面白い

一次元流れ

流体というものは形が決まってないことが非常に扱いづらい原因だ。まず、一番簡単なモデルとして、非圧縮性流体の定常流一次元モデルを考えます。ここでは流線というものを導入します。流れの中で流線は常に一定で流体要素(微小な水の塊)は常にこの上を通ります。流れは流線を横切らないので、流線で囲まれた流管も考えましょう。イメージとしては流し素麺みたいな感じ。実際に管路を考えてもいいのですが取りあえず摩擦は無しとしています。

流体を非圧縮とするとその代表は水です。空気は基本的には圧縮性ですが、特殊な条件では非圧縮として簡単化できることもあります。水も本当は圧力を加えると少しは縮むのですが、実用上は非圧縮として扱われることがほとんどです。非圧縮の水を主に扱う分野は水理学とも呼ばれ、河川や海の流れ、管路の設計などに応用され、土木や機械の分野では必修事項となっています。
【質量保存の法則→連続の式】
上の図は管路を模式的に示したもの。流体は管路の途中で湧き出したり、吸い込まれたりはしません。当然、管路の入り口から入った水は同じ量だけ出口から出て行きます。つまり、
  (流量)＝(単位時間に管路に入った流量)＝(単位時間に管路から出た流量)
流量は、平均流速×断面積です。つまり、単位時間にある断面を通過する水の質量を意味します。従って、
    u₁A₁＝u₂A₂=uA(任意の断面)…(1)
流量、つまり流れの速さ×断面積はどの断面でも一定。流れの速さは、断面積に反比例です。このことは野外活動で川を対象とする場合は必要な知識ですね。川幅が狭い所は流れが速い。渡るときには気をつけて下さい。
【運動量の保存則】
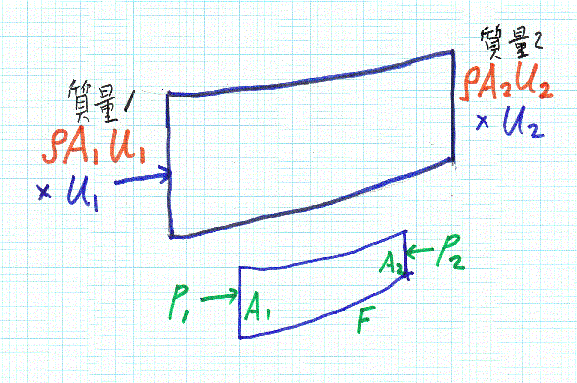運動量とは、その物体の質量に速度をかけたもの。運動の勢い見たいなものです。定常な流れでは、運動量も保存されます。
上の流管で、左から入って来る運動量を考えましょう。短時間に入って来る流量は、u₁A₁です。流入質量はこれに密度を掛けます。水の場合は非圧縮としてρ(一定)とします。また、またこの時の流速は当然u₁です。
従って、上に管で単位時間に流入(流出)してくる運動量は、 運動量in＝ρA₁u₁²
同様に流出する運動量は、 運動量in＝ρA₂u₂²
次に、この流管に作用する力を求めないといけませんが、下側の絵に示すように、 流管に作用する力は、p₁A₁－p₂A₂＋F
と簡単に求めることが出来ます。力Fはここには示されてませんが、重力だったり、遠心力だったりします。ただし、座標軸は流れの方向を正としています。
従って、運動量の保存式は、
ρ(A₂u₂²－A₁u₁²)＝p₁A₁－p₂A₂＋F…(2)
一般の力学では、(運動量の変化△（MV）)＝(力積F△t)となりますが、単位時間を考えているので力そのものとなります。ある意味では剛体の力学よりも楽かも知れません。
この運動量の保存則(2)式の応用例を下に示します。
消防用のホースから水が噴出しています。今、人が板を持って支えていますがどの位の力がかかっているのでしょう。まず、水の密度はSI単位系では、1000kg/m³。ノズルからの流速はu＝30m/sです。ノズルの径は20ｍｍなので0.02ｍ、断面積はA＝(0.02)²×π/4=10^－4・πｍ²、
運動量方程式を考えます。
出口の速度はu、板に当たった時は0です。つまり、 0－ρAu²＝－F、Fは板からジェットの出口に向かう人が押している力。ジェットは右向きのFの力を加えている訳です。
F＝ρAu²＝1,000×(10－4π)×30²＝90π＝283【N】
この力は28.9kg重で、小さな子供の体重程度なので、なんとか人一人で支えることが出来るでしょう。

【エネルギーの保存則】
　ここでは、単位質量当たりのエネルギーで考えます。水の微小要素については、単位質量当たりの運動エネルギーは、(1/2)u²となります。
次に圧力のする仕事を求めるには、流管を垂直に切る断面を考えて、
断面における単位時間当たりの仕事は、(仕事)＝(力)×(変位)＝pAu)　であり、同時にこの断面には単位時間当たりρAuの質量が流れ込んでいるから、単位質量当たりの仕事は、
  　(単位質量当たりの仕事)＝pAu／ρAu＝p/ρ　となります。
あと一つ残るのは、この単位質量の水の位置エネルギー。これは重力加速度を用いてgzとすれば出来上がりです。以上をまとめると、
  　(1/2)u²＋(p/ρ)＋gz＝一定…(1)
この式は流管内のどの断面でも成り立つわけです。

位置エネルギーが変化しない場合、
(1/2)ρu²＋p＝p₀＝一定…(2)
ここで、左辺第一項を動圧、第二項を静圧、右辺p₀を総圧(全圧)と呼んでいる。
また、p/w＝p/ρg＝Hを圧力水頭(m)と称し、(1)式を
  　(1/2g)u²＋H_p＋z＝一定…(2)
として、各項を長さの単位で表すことが土木の世界では一般です。これを水頭と称します。速度水頭、圧力水頭、位置水頭と呼んでいます。農業用の取水堰のことを頭首工(Head Work)というのもこれと関係しているかも。水位をせきあげして水頭を大きくするのですね。

水理学再入門

Eulerの運動方程式…三次元

普通、水理学や流体力学の教科書では、直方体の微小なサイコロdx,dy,dzモデルを使って、出入りする質量、運動量を勘定し微分方程式を導くのが筋でしょうが、それは、どの本を見ても書いてあると思います。ここではやや難解であることを覚悟して、ベクトル解析的な方法をトライしましょう。というのは、この後電磁気学を学ぶ際に、最終的の目標とするマクスウェルの方程式がベクトル形式で表現されているからです。

ちょっと、電気磁気学に寄り道すると、理論が出来る時点では電子の存在は知られていませんでした。電荷の流れが電流、ちょうど流体力学と同じ考えが用いられるのです。電流がプラスからマイナスに流れる。実はちょうど電子の流れと逆向きなのはそのためです。体系が確立してしまったので電子が発見されても電流の向きは逆には出来なかったのでしょう。

検査面とは空間内の適当な仮想の閉曲面。仮想の立体だ。そこに出入りする質量を考える。閉曲面内での質量の増加は、密度の変化を合計すれば良く、その合計は面か出入りする流体の合計だ。きわめて当然のことを言っているだけです。
まず、図の最初に出てくる▽とdiv（発散）という記号。これは微小な要素から湧き出す何かの量と考えれば良いのです。検査体積はたくさんの微小サイコロから出来ていると考えると、隣り合うサイコロから出てくる矢印は次のサイコロでは入ってくる矢印となって、互いに打消し合って、最終的には表面の部分しか残らないということを一般的に表したのガウスの定理です。この積分定理を用いると、適当な検査体積における体積分→面積分、面積分→体積分の変換が自由に行えることになります。

ガウスの定理を使えば(1)式の右辺も体積分に直せます。この時検査体積が任意のものであることがポイント。任意の形状で成り立つので積分記号を外した状態で等号が成り立つことになります。このようにして連続の式は簡単に導くことが出来ます。同じようにしてEulerの公式も誘導できるはずです。

水理学で頻繁に出現する　(D/Dt)=∂u/∂t＋u(∂/∂x)＋v(∂/∂y)＋w(∂/∂z) は、とても大事。流体の微小要素が時々刻々動いていることに起因しているのです。x,y,zの各成分に分解して記すると下記のとおりです。

水理学再入門

流れ関数

完全流体(粘性を無視)の2次元流れでは、流れ関数Ψが定義できます。渦度が0のとき、ラプラスの方程式を満たします。
まずは、2次元の流れを考えて、そこに流線を考えてみます。定常な流れを考えると流れの中に沢山の流れにそった線を考えることが出来ると思います。
次の渦度ベクトルωいうものを導入します。微分演算子∇と流速uの外積なのですが、形式的ですが行列式の形表わしておくと分かりやすと思います。今は2次元で考えているのでこのベクトルはk成分だけが残ります。方向は平面から鉛直上向きのベクトルですが、2次元流れなので大きさだけを考えればOKです。
ここで、流れ関数を左のように決めます。これを上の流線の式(1)に入れれば、dΨ＝(∂Ψ／∂x)dx＋(∂Ψ／∂y)dy＝0が求まります。dΨは全微分の形になっています。


渦度が0ということは流れ関数は△Ψ＝0、すなわちラプラスの偏微分方程式を満足します。

水理学再入門

速度ポテンシャル

渦がない完全流体では、速度ポテンシャルΦを定義することが出来ます。速度ポテンシャルの勾配(∇Φ)が流速を表します。ポテンシャルは、電気磁気学や重力の話でも出て来る重要な考えで。渦がない非圧縮流体とすれば、境界条件さえ決まれば、流れの状況が分かるようになります。つまり、流速が速度ポテンシアルで表されることと渦度がゼロということは同値です。

水理学再入門

力学も面白い

時間に関する微分

水理学再入門

力学も面白い

複素数と流体力学

流体の運動を解析するにあったては、まずは2次元の簡単な場合から取り掛かるのが自然であろう。二次元の場合の、速度ポテンシャルφと流れ関数ψの組合せ、これを組み合わせて作られた複素ポテンシャルw。結果は、実に美しい複素数の世界が構築されることになる。
目次

複素速度ポテンシャル

一様な流れ

湧き出しと吸い込み

二重湧き出し

複素速度ポテンシャル

流体の運動を解析するにあったては、まずは2次元の簡単な場合から取り掛かるのが自然であろう。二次元の場合の、速度ポテンシャルφと流れ関数ψの組合せ、これを組み合わせて作られた複素ポテンシャルw。結果は、実に美しい複素数の世界が構築されることになる。
複素ポテンシャルをwとしよう。  w＝φ＋iψ…(1)
ここで、φ； 速度ポテンシャル、  ψ； 流れ関数である。φやψは、座標x、yで微分すればその成分として、速度の成分（u、v）が現れて来ます。
だから、2次元座標で、x方向を実軸、y方向を虚軸として、φとψを結合した一つの複素ポテンシャルwを使って、複素平面上で統一的で美しい理論展開が可能になるのです。
(1)を微分してみよう。
   dw／dz＝lim△w／△z＝lim{w(z＋△z)－w(z)｝／△z　    (△z→0)
となるのだが、この微分dw/dzは△z→0の時、一定の値を取るという保証はない。ただそのような関数も存在しており、このような関数を正則関数と呼ぶ。微分可能な関数ということです。実は二次元の複素速度ポテンシャルを用いた華麗な理論は正則関数の場合だけにしか成り立たないのですが、結構実際の流体にも近似的うまく適応できる場合が多いようです。
先の(1)の微分は、dw/dz＝dφ/dz＋idψ/dz…(2)
で、zの近づき方によらないので、△z＝△x＋i△yで、△xか△yのどちらかを0に固定して、
△x→0としても、△y→0としても同じ値を取らないといけません。
   dw／dz＝∂w／∂x＝∂φ／∂x＋i∂ψ／∂x
   dw／dz＝∂w／i∂y＝∂φ／i∂y＋i∂ψ／i∂y＝－i∂φ／∂y＋∂ψ／∂y
正則関数では、この2つの微分は一致しなけらばならないので、複素数の実部と虚部を各々比較して、
      ∂φ／∂x＝∂ψ／∂y,    ∂ψ／∂x＝－∂φ／∂y …(3)
この式は、とても重要な公式でコーシー・リーマンの関係式と呼ばれるものです。

一方、速度ポテンシャルと流れ関数と速度の成分には次の関係があります。
∂φ／∂x＝u,    ∂φ／∂y＝v,    ∂ψ／∂x＝－v,    ∂ψ／∂y＝u   
以上のことをまとめると、
     dw／dz＝∂φ／∂x＋i∂ψ／∂x＝－i∂φ／∂y＋∂ψ／∂y＝u－iv
u＋ivを複素速度、u－ivを共役複素速度と呼ぶことになっています。

力学も面白い
複素数と流体力学

一様な流れ

具体例の最初は、最も簡単ない「一様な流れ(uniform flow)」から。

複素速度ポテンシャルは、w＝Az…(1)です。 Aは複素定数で、A＝a＋ib、   z＝x＋iy
従って、w＝(a＋ib) (x＋iy)＝ax－by＋i(ay＋bx)
wをzで微分すれば共役複素速度が得られる（dw/dz＝u－iv）。
正則関数だから、dw/dz＝∂w/∂x＝∂w/i∂y
dw/dz＝∂w/∂x＝a＋ib、すなわちu＝a、v＝－b、
同様にして、dw/dz＝∂w/i∂y＝－i∂w/∂y＝a＋ibで上と同じ結果になる。つまり(1)が正則関数という仮定は正しかったわけ。
つまり、(1)式はx方向の速さがu＝a、y方向の速さがv＝－bの一様な流れを示しています。
合成した速度は、U＝√(x²＋y²)とすると、
    u＝Ucosα＝a
    v＝Usinα＝－b
複素数では有名なEulerの公式がある。e^iα＝cosα＋isinα
この式を使うと、w＝Ue^－iα z…(2) これが、一様な流れを表す複素ポテンシャルの極形式による表示です。

力学も面白い
複素数と流体力学

湧き出しと吸い込み

原点を中心に湧き出してくる水、吸い込まれていく水を想定すればいいでしょう。
湧き出しの場合の複素速度ポテンシャルはチョット天下り的ですが、
    w＝m・log z (mは正の実定数)…(1)
これを微分すると、dw/dz＝m／z＝m／(x＋iy)、実は正則な複素関数は実数の関数と同じように微分できる性質があるんです。
     dw/dz＝m x／(x²＋y²)－i m y/(x²＋y²)
さらに、(x,y)＝(rcosθ, rsinθ)とおいて極座標に変換すると、
     dw/dz＝m r cosθ /r²－m r sinθ／ r²         ＝m cosθ／r－m sinθ／r
従って、u＝(m/r) cosθ、 v＝(m/r) sinθ
合成した流速は、U＝√ (u²＋v²))＝m／r、つまり角度θにかかわらず一定です。速度は半径に反比例しています。

次に半径r₁、 r₂の円を考えて、その円から出ていく流出量を考えると、
    2πr₁ (m／r₁)＝2π m
    2πr₂ (m／r₂)＝2π m
湧き出しが原点に一つしかなく、円周の長さは半径に比例、流速は半径に反比例、つまり円周から出ていく流量は半径にかかわらず一定になる。勿論そうならないのは、どこかの半径の円に流体がたまってしまうという不合理なことが生じるからだ。
吸い込みの場合は、全く同じ理屈が成り立ち、mを－mに置き換えればよい。
また、原点に湧き出しがないときは、w＝m log(z－z₀)、  z₀は、湧き出しの位置として、z'＝z－z₀という変数変換を行えば、同じ式が成り立つ。

力学も面白い
複素数と流体力学

二重湧き出し

この二重湧き出しというのは、原点の近傍に湧き出しと吸い込みが同時に存在するというとても変わった場合です。こんなものを考えて何の役に立つのでしょうか。そもそも同じ場所から湧き出しと吸い込みがあれば結局は何もないのと同じではないのか。まずは原点の近傍のx軸上(－δ, 0)に湧き出しがあり,原点(0,0)に吸い込みがある場合を考えます。

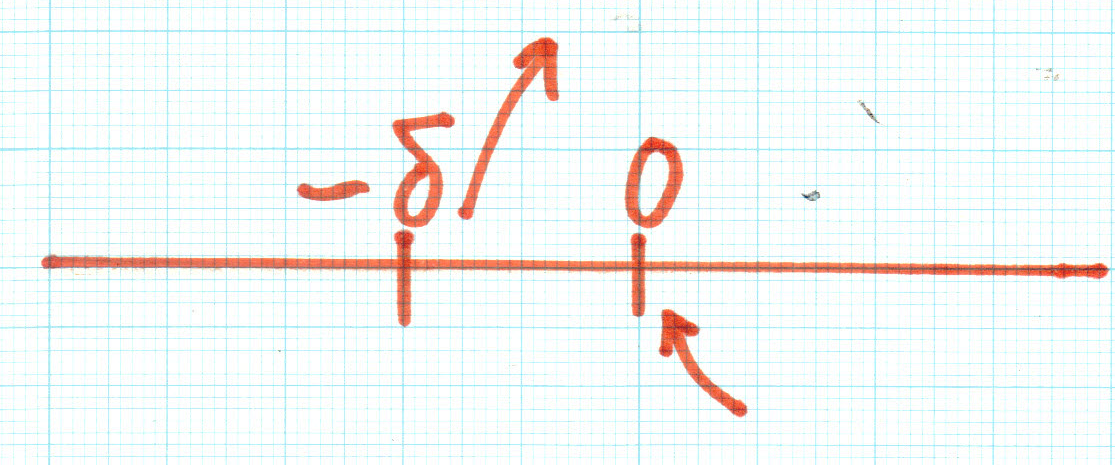
先の湧き出しと吸い込みの式を利用すれば、
    　wーmlog(z＋δ)－mlogz…(1)
     w＝lim_δ→0(mδ){log(z＋δ)－logz}/δ…(2)
ここで、チョット変な仮定ですが、δ→0の時、m→∞なって、μ＝mδは一定値を取るとします。
すると、　w＝μd/dz log z＝μ/z …(3)
    　w＝μ/(x＋iy)＝μ(x－iy)/(x²＋y²)
    　w＝μx/(x²＋y²)－iμy/(x²＋y²)、従って、w＝φ＋iψとすると、
     φ＝μx/(x²＋y²)、ψ＝－μy/(x²＋y²)となります。
ψ＝C(定数)とすると、－μy/(x²＋y²)＝Cから
x²＋y²＋(μ/C)y＝0となり、ψが一定の曲線はCをパラメータとする円群となりますが、これは流線を表します。

力学も面白い
複素数と流体力学