ゴルフの力学
目次
| ミート率について | 飛距離の力学(1) | ロフトと飛距離 |
| スイングロボットを造ろう | ゴルフのルール | ゴルフスィング動画 |
| オリンピック観戦記 |
ミート率について
ゴルフのプロはヘッドスピードを上げることよりも、ミート率を上げることをより重要視しているそうだ。この率と言う言葉、通常の打率、防御率、事故率などの使い方と少し違って、分かりにくい。定義は以下の通りだそうです。
ミート率＝ボールの初速/インパクト時のヘッドスピード ……(1)
なんだ、それなら初めから速度比とでも言ってくれればいいのに。まあ、そういうのが習慣となっているので今さら仕方がない。
アマチュアゴルファー、ヘッドスピードを上げるため練習に余念がないが、確かにいくらヘッドスピードを上げてもボールに伝わらなければ意味がない。ならば、きちんと芯を食ったあたりをすればいいのか。あるいはもう少しコツがあるのか。ちょっと、力学の知識を使って考察して見ましょう。
その前に、理想的なミート率は、ドライバーを含め長いクラブでは、1.5がベスト。上級者をめざすなら、1.4以上は欲しいと言われています。逆にバンカーでのサンドウェッジでは、0.9位になることもあるとのこと。わざとミート率を落とすこともテクニックということか。
まず、質量(力学では重さとは言わない)Mのヘッドが、速度Vでボールにぶつかります。
その結果、質量ｍのボールは初速ｖで飛び出します。
この時、クラブが理想的な振り子運動をしていれば、水平方向の成分だけを考えた場合、余計な力などは無視できます。
ここで適用するのは、運動量の保存則、高校の物理の領域です。
MV=MV´＋mv …(2)
ミート率の定義は、ミート率；μ＝v/V …(3)
あるいは、これを書き換えて、ｖ＝μV …(4)
おなじボールの初速なら、(3)からμはゆっくり振ってVを小さくした方が、μは上がります。確かにゆっくり振った方がボールの芯に当て易いので一理ありますね。また、(4)から、同じヘッドスピードなら、μが大きい方が球は飛ぶでしょう。プロがμに拘る理由も分かります。ところで、(2)から、
ｖ＝(M/m)(V－V´)＝(M/m)△V …(5)
ただし、△V=V－V´
V´は、インパクト直後のヘッドスピードです。良く、一般にはクラブはインパクト後も加速するように振れと言われますが、現実には絶対不可能です。しかも、減速の割合△Vが大きいほどｖが増える。つまり、よく飛ぶということになります。
更に、高校の物理では、エネルギーの保存法則も習っていました。
(1/2)MV2=(1/2)MV´2＋(1/2)ｍｖ2
(1/2)MV2=(1/2)M(V－△V)2＋(1/2)ｍｖ2
ところで、(V－△V)2＝V2－2V△V＋(△V)
(△V)2は、微小量なので省略します。
すると、エネルギー式から、
(1/2)MV2＝(1/2)MV2－MV△V＋(1/2)mv2
(1/2)ｍｖ2＝MV△V …(6)
ここから、ボールにエネルギーを与えるには、ヘッドスピードVと速度減△Vの積を最大にすればよいことになります。どうやらナイスショットのコツは、インパクトの瞬間にはシャフトからボールへの一切の力が加わらない完全な振り子の状態がベストのようです。つまり、ボールからの反作用がすべてヘッドの減速に使われる状態を目指せば良いことになりそうです。
【ミート率に関する追記】
実は、ミート率の理論的な最大値は次のように求められます。
質量Mのクラブヘッドが、速度Vで質量mのボールに衝突して、ボールが速度vでとびだします。その時、クラブヘッドはボールにエネルギーと運動量を渡して、自身の速度は△Vだけ遅くなるはずです。
運動量保存則とエネルギー保存則が成立します。
MV＝mv＋M(V－△V)……①
(1/2)MV2＝(1/2)mv2＋(1/2)M(V－△V)2……②
①は両辺にMVがあるので、M△V＝mv……③
②は、次のように書き換えられます。
MV2＝mv2＋M(V2－2V△V＋△V2)
2MV△V＝mv2……④
ここで、△Vは、Vと比べて相当に小さい(クラブが減速したことは感じないでしょう)ので。△V2は、無視できるとします。すると、③を④を代入して
2mvV＝mv2、つまり2V＝v
となりますから、ミート率μ＝v/Vは、μ＝v/V=2
つまり、エネルギーのロスが全くなくヘッドの持つすべてのエネルギーがヘッドの進行方向に伝えられれば、ミート率を最大2まで上げることは可能ということです。
でも、実際にはヘッドにはロフトがついていて上向きに力がロスするし、ボールの反発係数も1.0よりは小さく、それにボールを打つ時に出る音もエネルギーロスの原因です。プロでも1.5位がナイスショットとしているみたいです。
飛距離の力学(1)
まず、一番単純なモデルから。地面からボールを打ち上げます。下の図を参照下さい。ボールは止まっていて、原点(0,0)に静止しています。これをゴルフクラブでぶっ叩きます。ここからボールの飛距離を計算します。まず、ティーグラウンドでティーアップします。この時ボールの作用する力を運動方程式で表すと下記の通りです。座標軸ｙは、鉛直上向きに正、x軸はボールの飛ぶ方向を正とします。
d2x/dt2＝0……(1)
d2y/dt2＝－g……(2)
さて、クラブヘッドで速度Vでボールを叩き、ボールは速度ｖ、仰角θで飛び出します。ボールの質量ｍは、ここでは関係なし。バレーボールでもピンポン玉でもパチンコ玉でも同じですが、パチンコ玉では、軽量のドライバーのヘッドは、破損してしまうでしょう。さて、ここでショットを行います。初期条件は以下の通りとなります。
初期条件；ｔ＝0で、
(x,y)＝(0,0),
(dx/dt, dy/dt)＝(v cosθ, v sinθ)
θは打ち出しの角度です。(1)から、
dx/dt＝C1＝ｖcosθ……(3)
dy/dt＝－gt＋Ｃ2＝－gt＋v sinθ……(4)
もう一度、積分して、
x＝v cos・t＋C3＝v cosθ・t ……(5)
y＝v sinθ・t－(1/2)gt2＋C4＝v sinθ・t－(1/2)gt2……(6)
これは、有名な放物線です。(4)から、ボールが一番高く上がった時点で、dy/dt＝0、だから、この時刻がt＝v sinθ/g、ボールが落下するのは、この2倍の時間で、その時の飛距離xcは、t＝2 v sinθ/gを(5)に代入して求まります。
すなわち、xc＝v cosθ・2 v sinθ/ｇ＝(v2/g)sin 2θ……(7)
(∵ 2 sinθcosθ＝sin 2θ、2倍角の公式)
(7)を再度、書き直します。 xc＝(v2/g)sin 2θ …… (7)
sin 2θの最大値は1で、θ＝45°の時、飛距離は、最大でxc＝v2/g となります。
この時、ボールの初速は、v＝√(g xc) ですが、ドライバーの飛距離で200m(222yd)とすると、v＝44.3m、ミート率を1.4として、ヘッドのスピードは31.6m/s。少し遅すぎる気がしますが。ボールの初速を50m/sとして試算が上の図です。
ところで、この結果は現実問題として受け入れ難いでしょう。中高の理科で教わる通り、放物線の軌道は、打出し角が45°の時、飛距離が最大になります。角度が10°では、キャリーの飛距離は著しく落ちてしまいます。でも、ゴルフのボールは地面に置いてあります。ティーアップしたドライバーでも、地面から精々2cm位浮いているだけ。ヘッドは、ボールにほとんど水平に当たるはずです。上向きの45°に打つことなど絶対に不可能です。ということは、水平に当たってもボールが浮くのは、クラブのロフトのせい？
ロフトと飛距離
ロフトの影響を考えるため、超大型のクラブヘッドを考えて見ます。ロフト角θの塗り壁がボールに速度Ｖで衝突します。この時、塗り壁に固定した座標では、ボールが速度マイナスＶ、入射角θでぶつかることになります。反射の法則から、入射角＝反射角ですから、図に示すように水平に対して2θの角で上向きにボールは反射されます。ロフトの角度は2倍で利くのですね。反射したボールの速度は、エネルギーのロスがなければVですが、実際には、ボールや壁のわずかな変形でエネルギーが消費され、v＝eVとなります。eを反発係数と称します。本当はボールの方が止まっていて、ヘッドが動いているので、ボールはヘッド速度Vとボールの速度vのベクトル和(方向が一致してないから)で表されます。従って、ベクトル和V＋vの成分を計算すると、
水平x方向； v cos2θ＋V＝eVcos2θ＋V＝V(1＋e・cos2θ)
鉛直y方向； v sin2θ＝eVsin2θ
合力＝V√((1＋ecos2θ)2＋(esin2θ)2)＝V√(1＋2e cos2θ＋e2)
ここで、最初に求めたミート率を求めて見ると、
ミート率μ＝ボールの初速/インパクト時のヘッドスピード
＝√(1＋2e cos2θ＋e2)……(1)
ここで、完全弾性衝突を仮定すると、e＝1で、
μ＝√(2＋2 cos2θ)……(2)
また、ロフト角度０の場合は、
μ＝√(１＋2e＋e2)＝√(１＋e)2=１＋e
なんと、ロフト角0で、完全弾性衝突(e＝1)すれば、ミート率は2.0とすることが出来るんです。しかし、ロフト角0では、ボールはゴロしか出ませんし、eは１以下、プロでもミート率は1.5位が最大と言われています。eの値はボールの硬さ、ヘッドの材質、ヘッドスピード等色々な要素が絡むので理論的には求められませんが、ドライバーの反発係数は、0.83以下とルールで決められています。取りあえず0.8位と考えておきます。
(1)式でe＝0.8、θ＝10°なら、cos2θ＝0.94、μは何とμ＝1.77。プロ以上です。e=0.7でも、μ＝1.67となります。
今回の検討で、塗り壁君流のショットなら、ミート率、ボール初速ともかなりのプロレベルを越えてしまいます。。しかし、ボールの打出し角度はもう少し大っきくしたいですね。また、実際のショットは生身の柔な人間様が行うもの。もう少し、現実に近いモデルを造る必要があります。この際使える物理法則は、運動量の保存則だけ。エネルギーは、反発の際に生じるボールやクラブの変形で熱として逸散してしまいます。また、ボールの打出し角度も考える必要があります。これにはボールの回転を考えなければなりません。ボールの回転は周囲の空気との相互作用で初めて効果を現します。そのためには、若干の流体力学の知識も必要になります。
まず、空気による抵抗はボールにボールの進行方向の逆向きに働く抗力とボールの回転により進行方向と直角に作用する揚力に分けられます。
抗力については、ほぼボールの速度に2乗に比例する力となります。すなわち、
F＝CDv2
ただし、抗力はボールの飛距離を減らす方に作用します。アゲインストの風の中で打ったボールが飛ばないのと同じ理屈です。空気の薄い高山でゴルフをすると飛距離が増すのでしょうか。多分そうでしょうね。ボールのディンプルは、この抵抗を大幅に減らす工夫ということ。ボールは、放物線と比べかなり直線的に飛んだあと、急激に落下する形で飛ぶことになると思われます。
一方の揚力の方はどうなのでしょうか。ボールが曲がるのは、マグヌス効果と知られています。空気が無い所ではこの効果は出ないので本当に直線運動なのでしょうか。フックボールやスライスボールに悩むゴルファーも多いと思いますが本当に空気がない所ではボールは曲がらないのでしょうか。多分そうでしょう。ただ上向きの揚力は飛距離アップに寄与するでしょう。ただ低いボールでもカート道を転がって行けば相当距離を稼げることも事実。そうです、もう一つ飛距離に関係する大きな要素を忘れていました。ボールが着地してから受ける地面からの摩擦力です。摩擦力を無視したモデル。落ちたボールは等速直線運動で何か障害物に衝突しない限り永久に進み続ける。そう、カーリングのように小さな力でも結構な距離を進むでしょう。もちろん摩擦力は現実には0にはなりませんが、実際のドライバーショットでも低くて強い球は飛距離も大きいことはみなさんも経験から感じておられると思います。つまり、最大の飛距離は放物線の理論値より遥かに低い打出し角度なんだろうと推定されます。
スイングロボットを造ろう
どんな球を打てば良いかが分かれば、次はどのように打てば良いか。つまり、どんなスィングをすれば良いかが課題です。これば分かればだれも苦労しません。ここでは、スィングとは力学的見てどのような動作かの原理的な部分だけを見て見ましょう。
まず、思考実験としてゴルフロボットを考えて見ます。まず、スタンスを取った人から骨組みだけを取り出し、さらにスィングプレーンだけを取り出した平面を作ります。基本的には単なる振り子の運動と同じです。このスウィングプレーに沿って単純にクラブを回すだけ。実際にはこれに重力の作用も考える必要があるでしょうが、パターやアプローチでなければこの影響はとても小さい(微調整で調整が利く)ものとして無視します。するとこのスウィングの平面の向きは鉛直だろうが水平だろうが関係なくなります。そこで水平面内で重力の作用を考えないでモデルを作れます。
さて、体を捩じってクラブをあげていくプロセス、機械ならゼンマイというのか渦巻き状のバネを使えますが、人体を想定すると人の筋肉の動きをまねないといけません。ゼンマイなら巻く時に大きな力が必要でしょうが、ゴルフのテイクバックにはほとんど力は必要としません。人の筋肉は伸ばしたものが縮むだけ、縮んだ筋肉は自然と伸びるだけで力になりません。まして回転等不可能。
回転する力はトルクで表します。トルクは2つの同じ大きさの力で反対向きに引張れば得ることができます。この2つの力は互いに偶力と言って大きさは同じで、合力は0ですが、回転する力を生じます。体の軸に沿って筋肉を適切に使うことで最大の偶力を生み出すことが理想的なスウィングを作るコツなりそうです。軸を回転させることができる筋肉、足、腰、肩をどのように動かせば良いかですね。
この偶力を利用すれば、ゴルフのスィングはテイクバックで体の右サイドの筋肉で左サイドの筋肉を引張り(右利きの場合)、回転角を作り力を貯めます。ここで力を解放すると、今度は左サイドの筋肉が縮み、右サイドは自然と延ばされます(筋肉は自分からは伸びません)。簡単に言えばゴルフスィングとはこれだけのことです。インパクト時点で回転角はほぼゼロ(アドレスの時点)の戻り、それ以降は惰性で右サイドの筋肉が縮んで行くことになります。
図は、これを簡略化して示したもの。回転するバネです。普通のバネは縮んだ長さに比例して力が作用しますが、回転バネは回した分だけ力が発生します。微分方程式の形は全く同じ。変位x(長さ)が変位θ(回転角)に変わり、質量ｍが慣性モーメントIに変わります。慣性モーメントは、回りにくさを表す量。回転する各々のパーツの質量に腕の長さの二乗を掛け合わせて加えたもの。ここではまず一次近似としてクラブヘッドの質量Mだけを問題にします。本当はクラブのシャフトやクラブを振る人自身の慣性質量も考慮したいのですが、腕の長さの2乗の利きが大きいのでまずはこのようにしましょう。実は、この式バネの単振動の式です。スィングでは振動しませんが、練習には取り入れる価値はあるかもね。
バネの振動は、初等物理に現れる定番ですね。kをバネ定数(復元力)とすると、
m(d2/dt2)＝－kx、ω＝√(k/m)とすると、d2x/dt2＝－ω2x
これは、解が分かっており、x＝Asin(ωt＋δ)となります。Aとδは初期条件などから求めねばなりません。
全く同様にして、このモデルでは、
I(d2θ/dt2)＝－Kθ、I＝ma2
ω＝√(K/I)＝√(K/ma2)とすると
θ＝Asin(ωt＋δ)…①
これは、まさにバネで往復運動する振り子の方程式です。一般の振り子は重力だけ(ただし振幅は微小)が復元力ですが、この場合はバネが復元力となります。A＝θ0(テイクバック時の捩じり角)とするのは問題ないでしょう。
初期条件としては、t＝0で、dθ/dt＝0(切り替えし時はクラブは静止)です。
θ＝－θ0だから、δ＝－π/2
①をtで微分すると、dθ/dt＝θ0ωcos(ωt＋δ)…②
δ＝－π/2なら確かにdθ/dt＝0となります。
つまり、①の解は、θ＝θ0sin(ωt－π/2)…③と求まります。
また、dθ/dt＝θ0ωcos(ωt－π/2)…④
角度をテイクバックでθ＝－θ0まで捩じり、インパクト時にはθ＝0、それ以降にはプラスになるように角度を取りました。
インパクト時には、θ＝0だから、③よりsin(ωt－π/2)＝0
これよりスィング開始からインパクトまでの所要時間が求められます。
ωt＝π/2、つまり、t＝π/(2ω)、ω＝√(K/ma2)
この時、④から、dθ/dt＝θ0ω (∵cos0＝1)
この時のヘッドスピードv0は、回転角速度×半径ですから、
v0＝a θ0ω= a θ0√(K/ma2)
これから、ヘッドスピードが求まれば、回転バネの大きさを求めることができます。
V0の大きさはプロで50m/s、一般のアマチュアで45m/s位とされています。ヘッドの重さ(質量)は、200ｇ程度。aの値はシャフトの長さ＋腕の長さで1.5m位としますか。
K=mv2/θ0,、これからヘッドスピードを決めると対応するバネの強さを求められることになります。
バネの強さは、トルクTとして表され、回転の角度θ0に比例します。つまり、T＝Kθ0、T＝f×?となり、K＝ｆ?/θ0となります。?は対になったバネの間隔(例えば肩幅とか腰の幅)。とりあえずスィングロボットは設計できそうです。
スィングロボットのスウィング軌道は普通のゴルファーのスィング軌道に合わせます。スィング軌道がずれないためにはガイドレールのような拘束をつければ良いでしょう。重力の影響は。ヘッドを高さを2mまで持ち上げて、地面までおろすと、エネルギーの保存則から、mgh=(1/2)mv2から，v=√2ghからv＝6.26m/s、これはヘッドスピード45m/sと比べるとあまり大きくないのでとりあえず無視してます。
こんな簡単なモデルですが、上の検討から結構色々と教えられることがあります。まずは、ゴルフスィングは軸の回転だけで行けそうです。目標に向けた力は一切不要です。きちんと体を捩じれば、シャフトは自然にバネの力でインパクトの位置に戻ります。トップから捩じれをリリースすれば、自然と筋肉のバネで巻き戻るので余計な力は一切不要です。また、回転運動に伴う反作用を考えると体重の移動の必要性も多分理解できそうです(今後検討したい)。
【次の問題】
飛距離を稼ぐためには、捩じりの回転角をできるだけ大きくすること。しかし、人間の体の構造から、おそらくθ0をπ/2以上にすることはほとんど無理でしょう。でも、こんな方法で結構飛ばす人もいますね。でも、普通は手首を折りコックしてヘッドの回転を増やす方法を取ります。次はこの点を考えます。
上の図を見て下さい。外側の円がシャフトと腕を足した長さ。コックをするとヘッドは
D→C→B→Aと上がって行って、切り返した後は、A→B→C→Dとしてインパクトを迎えます。ヘッドは遠心力でどんどん外側へ向かいます。回転の半径が小さいときは同じバネの力でも回転の速度を速くすることができます。結果としてインパクト時のD点での速度を速くすることができそうです。数式で表すのは少し難しそうですが。グリップの部分は平面内でのピン結合でよさそうですが、実際のスィングではクラブをあげる時には体の構造上、ヘッドを開かざるを得ず、クラブのローテーションが加わります。
このモデルを力学的の解析するのは意外と大変みたいです。しかし、ゴルフスィングのコツは、結局、中心軸を固定したコンパスの動きのようにうまくいくようだ。
【複数バネの共同作業】
人の筋肉系というものは、筋繊維の収縮という引張りの力だけで構成されている。だからゴルフクラブを回転させるという比較的単純な動きも複数の筋肉群の共同作業で行われる。たとえば、下の図のようにクラブのグリップに近い方から、手首、肩、腰上部、腰(ヒップ)、足とあり、これらの部分を構成する筋肉が調和して働かないとスムーズな回転は不可能だ。
まず、手始めとして最も単純な２つのバネの連成を考えよう。しかも、回転バネではない直線のバネだ。
2つのバネは、それぞれ力Fが加えられると、
F＝－k1x1、F＝－k2x2
ここでk1、k2はバネ定数というもの。バネ定数はバネの硬さで、人の運動を考えると、作用点から遠いほど、硬くなり(k1＜k2)結果として大きな力を分担する。また、全体の変位は、
x＝x1＋x2
なので、x1＝F/ k1、x2＝F/ k2
から、x＝－(F/ k1＋F/ k2)＝－F(1/ k1＋1/ k2)
これは、形を変えると、
ｘ＝－kxとなり、k＝1/(1/ k1＋1/ k2)＝k1k2/(k1＋k2)
これが合成したバネのバネ定数だ。バネを直列に並べると上のようになる。バネが並列なら、簡単にk＝k1＋k2。
ちょうど乾電池の直列、並列と逆の関係になる。電気のコンデンサの直列、並列と同じだ。バネがたくさんあっても、
x＝∑xi、xi＝－F/kiだから、x＝－F∑(1/ki)
すなわち、F＝－kxとしたときのバネ定数は、k＝1/∑(1/ki)
しかし、上の図で、
x＝x1＋x2……①
かつ、F＝－(k1x1＋k2x2)
とすると、先端の重りの運動は、
md2x/dt2＝－(k1x1＋k2x2)……②
ここでωi＝√ki/m (i＝1,2)とすると
d2x/dt2＝－(ω12x1＋ω22x2)……③
となって、各々のバネは互いに別の固有周期を持った振動をしそうだ。しかし、取りあえず、ゆっくり引張って離して、その後の振動を考えなければ、合成バネ(１つのバネ)として取り扱っても大丈夫そうだ。
【頭が悪いとボールは飛ばない】
ゴルフのスィングは、正確さが第一。ところが人の頭の重さは、体重の1/10程度もあるそうです。体重60kgなら6kg、1リットルのペットボトルが6本。なまじ顔に目がついているため、かえって調節しようとして余計な動きをするようです。よく頭を動かすなと言われますが、動かすつもりがないのに動いてしまうのでしょう。でも、これだけ重たい頭が動けば再現性のある軌道を確保出来ないので、頭を動かさない練習はとても大切ですね。
スイングロボットの修正？
今まで検討してきたスゥイングロボット。実は人の体の構造から考えて一見不合理なところがある。肩からクラブの先端まで、これは体の正面に対して上下動、つまり鉛直方向しか動かしがたいのです。では、胴体～腰は当然水平方向の円運動。合わせると結果として斜めに傾いた円運動になるんです。ここを理解しないとどうも体の使い方が分からなくなって、ミスショットの連続となってしまいます。上で述べた理屈は多分正しいのでしょうが、変に理屈で考えるとかえって分からなくなるかも。無理なくスムーズに振れば嫌でも円運動になるものです。
ゴルフ川柳
ゴルフをネタにゴルフ以外のことでも楽しみましょう。これも「ゴルフ道」の一部。
●ゴルフ川柳
(1).フェアウェイでミミズをよけて6インチ
(2).バンカーはスコアの貯金をするところ(銀行マン)
●ショートショート
(1)凄いカラス型ロボットを開発しました。空中であなたの打ったボールをキャッチして、グリーン上のカップの中に直接運びます。別に落ちたボールを拾い上げてもいいよね。簡単にホールインワンやアルバトロスもできます。カラスはあなたが自分で運ばなくても、自ら飛んでゴルフ場に直行します。プレーが終わったら、自分で飛んで倉庫に帰っていきます。あなたも同伴競技者もそのカラスが本物かロボットなのが見分けがつきません。ネットで予約振込して下さい。
ゴルフのルール
【ぺリア方式とは】
ぺリア方式を簡単に説明すると、その日1日だけのハンディキャップ算出方式ということです。基本的に日本ではアンダーハンディ戦は一般的でなく、公式なハンディキャップを所有しているゴルファーはほとんどいません。そのため、ハンディキャップを所有していないゴルファーがプレイするゴルフコンペなどにおいて、ぺリア方式での計算方法が用いられます。
ぺリア方式の計算方法
ぺリア方式での計算方法は、隠しホールの合計に3を掛けて72を引き、そこに0.8を掛けます。グロススコアからそこで計算された数字を引けばネットスコアとなります。企業内コンペなどでよく採用される方式ではありますが、比較的複雑な算出方法のため、しっかりと理解している人は多くはいません。しかし、覚えておくといざという時に役に立つことがあります。
2018年2.28、私が優勝した時の場合
隠しホールでのスコアの合計4+5+9+7+10+5＝40
｛(4+5+9+7+10+5)×3－72｝×0.8＝38.4
103(グロス)－38.4＝64.6→72－64.6＝7.4アンダーでの優勝となしました。
隠しホールは６つあり、隠しホールのパーの合計は、3+4+5+4+5+3＝24です。
隠しホールでもっと叩けばもっとすごいハンディも出そうです。
もし、これが新ぺリアで隠しホールの合計が、80ならば
｛80×1.5－72｝×0.8＝38.4で上と同じだけど
隠しホール(12個ある)のパーの合計は、倍の48だから、もし合計が60なっていたら
｛60×1.5－72｝×0.8＝14.4
103(グロス)－14.4＝88.6でむしろブービー候補かもね。
ぺリア方式での計算で出したスコアは相当に運に頼った面があるため、一部では不公平という声もあります。そこで現在では、隠しホールを12に設定したダブルぺリア方式や、9つの隠しホールによる新新ぺリア方式と呼ばれる計算方法がよく使われています。うまい人が上位に行くのが公平か、だれでも優勝のチャンスがある方が公平か、コンペの性格で使い分けていくのが良いようです。
ゴルフスィング動画
ゴルフのスィングはやはり動画を見てみるのが速い。
橘田、高松志門、 規奥田靖己、
高松志門
奥田靖己
松山英樹プロDriver Shot
石川遼プロDriver Shot
宮里藍プロDriver Shot
原英莉花Driver Shot
笹生優花
渋野日向子
アーニーエルス
アディティ・アショク Aditi Ashok
ゴルフの力学 中井学
青山加織
ゴルフの力学 ∫∫∫∫∫∫∫∫ ∫∫∫∫∫∫
オリンピック観戦記
埼玉県では、東京2020大会でオリンピック4競技（バスケットボール、サッカー、ゴルフ、射撃）、パラリンピック1競技（射撃）が開催された。
霞ヶ関カンツリー倶楽部は、1929年に霞ヶ関村（現在の川越市内）に開設された、埼玉県最初のゴルフ場。1957年には日本国内で開催された初のゴルフの国際大会であるカナダカップ（現在のワールドカップ）第5回大会が開催。また、1971年以降、日本ジュニアゴルフ選手権競技の会場として使用されて来た。
2013年、日本オリンピック委員会加盟団体である日本ゴルフ協会の調査・選考の結果、2020年東京オリンピックで、ゴルフ競技の会場になることが決定。その後、完全なプライベートクラブ（日曜日は会員であっても女性がプレーすることは許されない）であることから、公益性の観点、オリンピック憲章に明記されている遺産としての価値を日本国民が享受できるのか、などの議論が起きている。大宅映子以下日本ゴルフ改革会議は、同カントリークラブを選定したプロセスの説明が全く不十分である点や、東京からのアクセスの悪さなどを指摘した上で、他の競技会場とも近く、誰もがプレー可能なパブリックコースで、実際に2016年東京オリンピック構想ではゴルフ会場予定地とされていた若洲ゴルフリンクス（若洲海浜公園内）を推す提言を2014年10月にまとめた。さらに倉本昌弘は2014年10月14日付の「週刊ゴルフダイジェスト」で、ゴミ埋立地での開催というエコロジー性も挙げながら若洲開催の利点を述べた。
これに対し、永田圭司は2014年10月14日の「第1回日本ゴルフビジネスフォーラム」で、（若洲のような）都営施設の場合は東京都の予算で整備や改造が行われる一方、「民間の霞ヶ関CCの場合、国や都からは一切、出ない」（組織委員会による負担の可能性は示唆）という点も挙げながら、国際大会の実績・36ホールが必要の規模（若洲は18ホール）・観客収容人員などで若洲は基準を満たさないとして、「会場の見直しは100%ない」と述べた。
2017年3月、臨時理事会で女性会員の受け入れを決議した。倶楽部側では「東京オリンピックは無関係。女性会員を認めるのは世界的な流れ」としている。
男子は米国のXander Schaffeleさんがトータル(四日間)でマイナス18アンダーで優勝。二位のRory Sabatiniのマイナス17アンダーも凄い。四日目に一機に追い上げて来た。銅メダルをかけたsudden-death playoffは何と7人の戦いに。期待の松山英樹は最後まで優勝争いに絡んでいたのに、惜しくもメダルを逃した。
女子は米国のNelly Kordaが優勝。稲見萌寧はsudden-death playoffで見事銀メダルをしとめる。インドのAditi Ashokは終始メダルの絡んだプレーを見せていたが惜しくもメダルを逃した。
ベクトル解析入門
水理学や流体力学において、ベクトル解析の知識は極めて重要である。そういう私も、水理学はEulerの運動方程式やベルヌーイの定理程度の基礎でものたりたわけで、何を今さらということもありますが、ベクトル解析自体が流体の本質を解明するために発展して来たものなのです。ちょうど、微分積分の発展が質点系の力学と一緒に車の両輪のように発展してきたことと全く同じです。更に、電磁気学も電荷の流れをちょうど流体として扱うため、ベクトル解析の理解が不可欠なのです。最終的には、電磁気学のマクスウェルの式まで到達したいと思います。現象をどのような式で表現するかは現象を理解するうえで極めて大切です。そのため、若干の寄り道をしてベクトル解析の基礎をマスターしたいと思います。
まずは、一番良く見かけるgrad, div, rotについて。これを見ただけで逃げ出してしまう人もいるかも。三つとも同じ記号では∇と書きます。一種の微分みたいなもの。ただし、これは数値ではなく、いわゆる演算子というもの。ちょうどd/dxとか∂/∂xと同じ。すなわち、∇＝(∂/∂x, ∂/∂y, ∂/∂z)です。これは、3成分を持った1種のベクトル見たいなもの。∇f=grad f。つまりスカラー関数f(x,y,z)にかければ、ベクトル×スカラーで結果はベクトル。勾配と呼びます。∇・A＝div A。ベクトルAに内積として掛ければ、結果はスカラーで発散と呼ばれます。最後に∇×A＝rot Aは、回転と呼ばれ、外積なので結果はベクトルです。
また、∇を組合わせた次の公式も重要です。
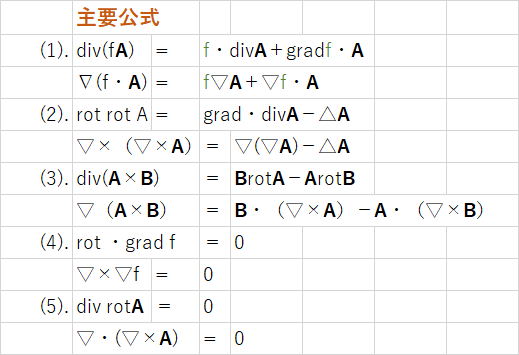
ベクトルに関する積分の公式もあります。
部分積分と置換積分
物理や理工系の専門書を頻繁に数式が出て来ます。
【部分積分】部分積分
関数f(x)とg(x)がある時、
∫f g’ dx＝f g－∫f’ g dx …(1)
これが、部分積分の基本公式。
例えば、I＝∫log x dxを求めたいとします。
この時、f＝log x、g＝ｘと置きます。ｆは積分は出来ないけど、微分したら1/xとなります。
gは微分すると1です。
I＝∫log x dx＝x log x－∫(1/ｘ)ｘdx ＝x log x－ｘ＋Ｃ …(2)
(1)式のもとは、微分法の積の微分公式 (f・g)＝f’g＋f g’ です。
【置換積分】置換積分
関数f(x)とg(x)がある時、g(f(x))の積分を考えます。
∫g’(f(x)) f’(x)dx＝g(f(x))＋C …(1)
これも、微分法の合成関数の微分からきています。
(g(f(x)))’＝g’(f)・f’ ; 全体をｆで微分して、次にｆをｘで微分します。
(1)では、迷わずにf(x)＝hとおいてみます。f’(x)＝dh/dxだから、
∫g’(h)) (dh/dx)dx＝∫g’dh＝g(h)＋C