scienceの部屋---はじめに

色々と観察し、仮説を立てて、実験などで検証する。この立場には自然科学も社会科学も区別はないと思う。なんでもやってみよう。物理、化学、地質学、生物学、経済学、社会学、宇宙、生命、数学、文学、芸術、ゴルフ理論、将棋、何でもありで行きましょう。特に最近は色々な学問の境界に属する課題が非常に面白いと思います。全体の見通しを良くするため、目次を付けてみました。興味のある話題から、別の話題に自由に飛び回って頂ければと思います。(2018.6.2)
【追記】
なんでもあり？　それ、哲学と同じかな。英語では、自然科学の博士をDocotor of Philosophy　何て言っているから、哲学と科学はもともと同じものだったんだろう。自然科学の知識が膨大になり枝分かれして全体像が見えなくなっている。専門の細かい枝分かれした部分は、今後AIが補助して来るので、今後我々は、総合的な見方で全体像を把握していく努力が必要なのでしょう。(2020.11.1)

Scienceの部屋目次

地球の歴史・生命の歴史	人類の歴史	物理の世界	化学の世界	相対性理論入門
生物の世界	数学の部屋	力学も面白い
経済の話	技術開発のお話	哲学・社会学の部屋
最近流行している言葉	熱力学とエントロピー	量子力学の世界
相対性理論入門	SF小説の世界

地球の歴史・生命の歴史…地球の歴史46億年の実態が最近どんどん分かってきている。それを学べば世界観も変わってくるはずだ。

人類の歴史…人類誕生の謎。最近研究が進んでずいぶん新しいことが分かってきました。これからの人類の進むべき道への示唆となるものの見方も変わってくると思います。ただ「人類の歴史」については「歴史の部屋」への移転も考えており、そちらからもアクセスできます。
人については、今までサルの仲間としてくくられていた類人猿たちが遺伝子から見て人とほとんど変わらないことが明かにされて来ました。人類の歴史の中には彼等も含めて考えないといけないようだ。サピエンス、ボノボ、チンパンジー、ゴリラ、オランウータンは皆人です。ネアンデルタール人もジャワ原人もね。

物理の世界…自然科学と言えばまずは物理でしょう。物理の基本を見直して見ると世の中に見方が変わるかも。物理は江戸時代は「窮理（きゅうり）」とも呼ばれていたとか。物事の真理を探究すると言う意味。仮説を立てて次々の検証していく。でも、検証と数学でいう証明とは同じではない。つまり物理学で言う仮説はある意味いつまでも仮説の運命を背負わされているんだ。

化学の世界…化学という言葉は江戸時代には舎密（せいみ）と言ったらしい。日本の近代化には不可欠な学問だったんだ。中学高校で習う化学。先生は白衣着ておおお厳かに実験をする。先生の手はまるで魔法使い。生徒が同じ実験しても必ずしも上手くいかないぞ。まさに錬金術の世界でもある。でも、最近科学の世界変わってきている。量子力学を取り入れた。酵素が主役の生命科学なんか。化学は決して暗記科目ではないようだ。

生物の世界…生き物の世界は知れば知る程深い。一つ疑問が解決すればまた新たな疑問が。遺伝子の研究が進んで新しい知見がどんどん出てくる。今までの生き物に対する見方も、人類の進化の見方も大幅な変更が迫られているようです。

相対性理論入門…科学をやるなら一度は触れて見たい。でもどこまで分かるかな。

SF小説の世界…SF小説というもの結構科学を先取りしており、現代科学の課題や方向性がよく分かる。

力学も面白い…
経済の話…
哲学・社会学の部屋…
最近流行している言葉…
技術開発のお話…

裸坊達の部屋に戻る 　

相対性理論

20世紀の物理学の2大成果としては、相対性理論と量子理論が挙げられるでしょう。量子論の方は大勢物理学の大家が成果を少しずつ積上げて行ったものですが、相対性理論の方は、天才アインシュタインがほとんど一人で作り上げていった感じのものです。相対性理論は、最初に完成された特殊相対性理論とそれから十年あまりの努力の結果生まれた一般相対性理論で構成されています。後者は、法則を記述するための新しい数学理論が必要だったので、数学嫌いの彼が、著名な数学者の助けを借りて猛勉強して、十年近くかけやっと完成したものだそうです。一生の間これほど勉強したことは無かったと本人も振り返っているそうです。真理を知ろうとする強烈なワクワク感があったのでしょう。

さて、最初の特殊相対性理論の方は、そんなに難しくありません。他の物理学者達も一歩手前までは達成していたようです。発想の転換が革命的だったのですね。それまでは、宇宙は、絶対静止した空間に単一の時間と言ったものがあるという前提がありました。でも、そのような前提では、光速が不変であることと、電磁波のマクスウェルの方程式が座標変換で不変にならないことを説明しきれないことから、時空(時間と空間の組合せ)が相対的にしか決められないことに気がついたそうです。
      このサイトでもいずれ、その具体的内容を紹介したいと思ってますが、もう少し中身を掘り下げるとともに、表現方法も検討したいので、もう少しお時間を下さい。

相対性理論入門

物理の世界

万有引力の話

万有引力の話	万有引力の話(2)…連続体の場合	地球エレベータ
無限に広がった平面の場合	平板コンデンサー内部の電界と容量

F＝Gm₁m₂／r² …(1)
これぞ有名なニュートンの万有引力の公式です。これを地球上の物体に当てはめれば、

万有引力定数　G＝6.670×10－11 Nm2／kg2                      地球の質量　　M＝5.972×1024kg                      地球の半径　　r＝6,371km＝6.371×106ｍ

ここで、リンゴ(一つm＝100g＝0.1kg)を用意しましょう。
この林檎に働く力はいわゆる重力です。重力は当然ニュートンの有名な万有引力の式(1)から求まります。リンゴが例え上空1kmにあっても地球の半径は大きいので、(1)式の中のrは変わらないとしていいですね。m₁は地球の質量、m₂はリンゴの質量です。従って、(1)より
F＝6.670×10^－11×5.972×10²⁴×m₂／(6.371×10⁶)²  　＝0.981×10^{(－11＋24－12)}× m₂
　＝9.81 m₂
9.81m/s²は、地球上での重力加速度。従ってm₂＝0.1kgだから
F＝9.81 m/s²×0.1kg＝0.981N
つまり、0.1kg重です。ここまでは、復習です。100gのものが0.1kg重になるのは当然ですね。
万有引力の計算式自体は簡単ですが、天体の物理ではやたらと大きな数が出てきてまちがいやすい。下記はBasicで書いたプログラムの一例。最近教育の現場からは何故か消えてしまってますが、どうやってプログラムしているのでしょうか。Excelでも出来るけど、やはり不便だと思います。質量や距離を入力したら、ぱっと引力を計算してくれることが練習になると思うのですが。
10 REM 万有引力を計算してみよう
20 LET G=6.67E-11 !万有引力定数＝6.67×10^(-11) Nm2/kg2
30 REM 地球の質量 M=5.972×10^24 kg →5.972E+24
40 REM 地球の半径 R=6,371 km→ 6.371E+06 (m)
50 INPUT PROMPT "質量M1=":M1
60 INPUT PROMPT "質量M2=":M2
70 INPUT PROMPT "距離R=":R !地球の半径はR= 6.371E+06 (m)
80 LET F=G*M1*M2/R^2
90 PRINT "F=",F,"N","→kg m2/s2"
100 END
公式が与えられれば、地上でも宇宙でも2つの物体の間に働く距離は計算で求めれれます。 でも、万有引力はすべてのものに対等に働くので、リンゴが2つあれば、このリンゴ同志も互いに引きあいますね。ふだん考えることはありませんが。もちろんこの答えも簡単に求まります。例えば2つのリンゴが10cm(0.1ｍ)離れているとしましょう。(1)式を使えば、
F＝6.670×10^－11×0.1×0.1／(0.1)²
　＝6.67×10^－11N＝0.68×10^－11kg重
こんな小さな力は問題にならないことは当然です。

では、次にこの2個のリンゴが宇宙空間に10cm 離れておかれていたらどうでしょう。宇宙空間では、万有引力だけが有効に働く力です。地球も太陽も塵やガスが集まってできたものと考えられています。このリンゴが等加速度運動で、5cm (相手方のリンゴも5cm動くから)の距離を動くと仮定して見よう。
この時の加速度はF/m=a=6.67×10^－10m/s²　)
X＝(1/2)× 6.67×10^－10 t²＝10 cmから、(X=(1/2)α t²)
t＝√ (2x／a)＝√ (2×0.5／6.67×10^－10)＝0.387×10⁵ s ＝0.387×105s÷60÷60÷24＝0.44日
v＝at＝6.67×10^－10m/s2×0.387×10⁵＝2.58×10^－5m／s
取りあえず半日ほどで衝突するのですが、衝突速度はやけに遅いです。
でも、万有引力は(1)式から距離の2乗に反比例して大きくなります。2つのリンゴが近づくにつれて働く力は急激に大きくなります。上の計算は明らかに過小な見積もりです。2つのリンゴが衝突する瞬間は何と力Fは無限に大きく（距離が零だから）なってしまします。取りあえずリンゴが合体するところまでは予測できます。しかし、無限大の力を受けたリンゴがどうなるのか、(1)式から得られる情報だけでは予測できません。
地球も他の惑星も微惑星の衝突から生まれたとされています。その時の微惑星の衝突は、ここで述べたリンゴの衝突と変わらないですね。どのように衝突したのか知りたいですね。ニュートンの有名な万有引力なんてみんな知っていると思っていますがよく考えると分からないところも沢山あるようです。
【追記】ここで、述べてきたNewtonの万有引力の式は、質点系に対するもの。リンゴはある程度の大きさがあるため、接触する時は中心まで一致するわけではなく、各部分部分に異なった引力が働いており、力が無限大になることはありません。また、パソコンのキーボードに接触する時、距離がゼロですが、引力が無限大になり指が離れなくなることなど絶対にないですね。指にもキーボードにも形を保とうとする分子的な反発力があるので心配ないわけです。でも、距離が極限としてゼロに近づいた時、どうなるのか考えてみるのも悪くないでしょう。

物理の世界
万有引力の話
scienceの部屋

万有引力の話(2)…連続体の場合

　 万有引力の公式は次の通りであった。 F＝GmM／r² …(1)
ここで、mは今まで通り質点としておき、Mを連続体の質量としよう。簡単な場合としてMが半径 a の中空の球殻の場合を考える。地球を考えても、実際にはマントルや核などと成層構造をしているけど、基本的に中心に全質量が集まった質点として取り扱っても良いようだ。実際に地上での力学では、重力は下向き地球の中心を向いているとして計算しても何の問題もない。中が伽藍洞(がらんどう)の球殻でも多分同じだろう。つまり、m が球殻の外側にあるときはこのことを確かめるだけだ。
だけど、mが球殻の内側にある時は、そう簡単ではない。質点mは、半径aの球殻の中心を通り、垂直な位置に置かれています。球殻と質点mの距離はrとします。2つの場合に分けて考える必要があります。(ⅰ)質点mが球殻の外側にある時、(ⅱ)質点mが球殻の内部にある時の2つだ。球殻の表面積はS＝4π a²、 μ [kg／m²]を単位表面積当たりの質量とすると、M＝μS＝4πa<>sup2μだから、μ＝M/(4πa²)となる。


(ⅰ) 質点mが球殻の外側にある時
球殻の中心から質点mまでの距離をRとして、球殻がmに及ぼす引力を算定する。まず、球殻をOPに垂直な厚さdxの薄い円環に輪切りにします。この中心からxの距離にある円環上の微小部分dsがmに及ぼす引力の大きさは、
df(微小部分)＝Gmμds/r²
ところが、円環は軸OPに関して対称だから、OPに垂直な成分は互いに打消し合ってなくなる。だから、
df_{(微小部分のPO方向の成分)}＝df_{(微小部分)}×cosφ= df_{(微小部分)}×(R－x)/r＝Gmμds/r²×(R－x)/r
＝Gmμ(R－x) ds/r³
円環全体の合計の引力は、
df_{(円環全体の合計の引力)}＝2πy・df_{(微小部分のPO方向の成分)} ＝Gm・2πyμ(R－x) ds/r3
ここまで、準備すれば求める引力Fはdf_{(円環全体の合計の引力)}を合計すれば良い。
すなわち、球殻全体ではF＝∫df_{(円環全体の合計の引力)}となるわけだが、実はこの積分が大変そうだ。どの変数に着目するかだが、rを取れば、r＝R＋a～R－a、xに着目すればx＝－a～a、他にθをパラメータとしてθ＝0～πとする方法もありそうだ。そのようにして変数を一つにしないと積分はできない。
まずは、rに着目。dx/ds＝sinθ→ds＝dx/ sinθ、y＝a・sinθからsとyを消す。
一方、r²＝y²＋(R－x)²＝y²＋R²－2Rx＋x²＝a²＋R²－2Rx＝a²－R²＋2R(R－x)であるから、
2r・dr/dx＝－2R、　∴dx＝－r dr/R、R－x＝(r²－a²＋R²)/(2R)
df(円環全体の合計の引力)＝Gm・2πaμ・sinθ×(r2－a2＋R²)/(2R)×dx/ (r³sinθ)
   　    ＝Gm・πaμ・(r²－a²＋R²)/( R)×(－r dr/R)×1/ r³
   　   　＝－Gm・πaμ(r²－a²＋R²) /(r²R²) ×dr
   　    =－(Gmπaμ/ R²){1－(a²－R²)/ r²}dr

   　検討の結果、点Pが球殻の外側にあれば、どの、球殻からの引力も球殻の全質量が球殻の中心に集まったものと見做すことが出来、結局はその合計を取ればよいことが確かめられました。ところで、ここで結構間違いやすいのが積分の範囲。aからbに積分するのと、bからaに積分するのでは符号が反対になってしまいそうだ。ここでは基本はあくまでもdxを全部集めたとして、x軸上を－a～＋aまでのdxについての値を積分すると良い。このようにすればdxは微小でも正の値を保っている。変数を変換してもこの符号の向きを忘れては積分の結果の符号が反対になったりして??となってしまう。

(ⅱ)質点mが球殻の内部にある時

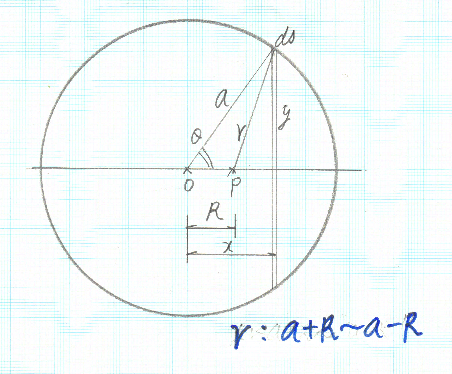
この場合、積分の範囲がa＋R～a－Rに変わること。これを実行するとなんと球殻内部では引力が零となってしまいます。球殻の周りからの引力が互いに打消し合って、全体として引力が零になってしまうわけだ。

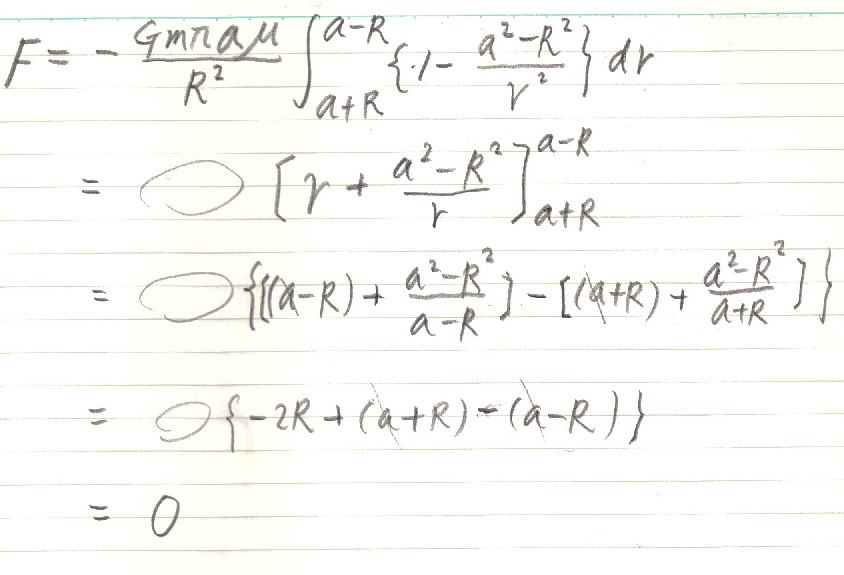
すなわち、F＝∑f＝(Gm’/R²)∑m=(Gm’/R²)∫dm＝Gm’M/R²
   　巨大な球殻の宇宙ステーションの中は無重力状態なわけで、まあその点は理解して頂けそう。しかし、地球の深部は高温超高圧であることが知られています。宇宙ステーションの中にもう一つ少し小さな宇宙ステーションを建設していきこれを繰返して行っても中心は無重力が残るのでしょうか。地球の中に空洞があって別世界が存在しているということは昔のSFではありましたが。球殻がもし剛体でなければ、こうはならないのでしょうか。球殻の中に水を入れた場合はどうなるでしょうか。

物理の世界
scienceの部屋
万有引力の話

地球エレベータ

次の、思考実験は地球の中心を通る竪穴を掘り、そこに物体を落とした時にどんな運動をするかという壮大なプロジェクト。球体は地球でなくてもいいので、将来人類が地球から宇宙へと脱出するような時代にはこんなプロジェクトもありかも。とりあえず、地球の平均密度をρ(kg/m³)、質量m(kg)の物体を地球の中心から半径r(m)の位置に置いてみる。先の検討から、物体に作用する引力は、半径rの内側の質量のみ。つまり、

   　      　    M'=(4/3)πr³ρ
であるから、この物体に働く引力はいつも地球の中心Oを向いており、その大きさは、
   　      　    f＝GmM'/r²
ところが、地球の総質量Mは、rをRとすれば良く、M=(4/3)πR³ρ 、M'＝(r³/R³)M だから、
   　      　    f＝GmM/R³×r
つまり、    　f＝kr、k＝GmM/R³;　　 力が、常に中心からの距離に比例して、なおかつ中心に向かっているということで、これはバネの単振動(md²x/dt²＝－kx)と同じだ。
この単振動の周期は、T=2π√（m/k)となる。

この振動は非常に高速だ。わずか1.4時間程度で地球を一往復。平均時速9000km/時となる。ただ、この周期は、重力加速度の平方根に反比例するので月を対象にすれば2.5倍ぐらいに増えてしまうがまあ、実用的な値だろう。月ならば穴を掘ってもマグマは出てこないだろう。

物理の世界
万有引力の話
scienceの部屋

無限に広がった平面の場合

次に考えるのは無限に伸びた平面(質量を持った)が、そこから距離a(m)のところにある点Pにある小物体(質量mの質点)に及ぼす万有引力を求めようというものです。全く空想上の仮定みたいだけど、半径約6400ｋｍ地球の上空10km(高度1万m)に何か物体が浮かんでいる情景は、ほぼこんなものでしょう。なお平面の質量面密度をμ(kg/m²)と仮定します。

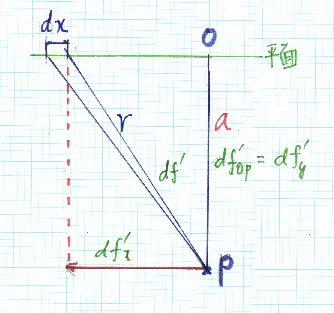
点Pから垂線を下ろしてその足をOとしましょう。Oを中心の平面上の同心円がたくさんあると考えます。その中から微小な幅dxのリングを選んで、微小中心角に対応する長さをdsとして、平面の微小要素と質点mの間の引力は、
   　      　    df'＝Gmμdxds/r²
この力はx方向（リングの径方向）の力は、互いに打消し合ってしまうので、OP方向の成分だけ考慮すれば良い。
   　      　    df'＝Gmμdxds/r²・(a/r)
だから、リング全体としては、df＝Σdf'_OP＝Gmμdx/r²・2πx(a/r)＝Gmμadx/r³・2πx
ここで、r²＝x²＋a²、だから2rdr/dx＝2x　→dx/r＝dr/xとなるから、
   　      　    df＝Gmμ2πadr/r²
平面全体が質点mに及ぼす引力は、dfをすべてのリングのついて積分すればよいので、dxについて0～∞まで積分する。変数xをrに変換したので、drにつてa～∞まで積分すれば良い。
   　      　    f＝∫_a^∞df＝Gmμ2πa∫_a^∞dr/r²＝Gmμ2πa[－1/r]_a^∞＝Gmμ2πa×(1/a)＝2πGmμ(一定)…(1)
つまり、この平面の上にある物体には高さにかかわらず、同一の引力が働くことが分かります。高さが2倍になれば、同じ立体角での平面上の面積は4倍(対応する質量も4倍)になりますが、距離が2倍になるのでそれによる引力は1/4になり、結局高さに依存しないことが分かります。
ここで、チョット不思議な気がするのは平面上の質量分布は無限に広がっているので、その質量の合計も無限に大きくなるような気がするのですが、その値は有限で収まっています。結局xが大きくなる遠くの方の微小平面の引力は、鉛直方向の成分が小さくなるので効果が小さくなってしまうのです。だから、実際には平面は無限でなくてもある程度大きなものなら無限だとみなしても差し支えないということです。平面を地球の表面に見立てると、地上に存在する質量mに対する引力はmgです。つまり、地球上の物体にはすべて重力加速度gが作用することを証明したことになるんです。
地球の質量をM、地球の半径をRとすると、g＝GM/R²…(2)、また、(1)式の力が地上での重力ですから、
   　      　    mg＝2πGmμ、これと(2)式の関係から、μ＝M/(2πR²)
つまり、最初に仮定した面密度はμ(kg/m²は、地球の質量の半分を地球の投影面積で割ったものだと分かります。

物理の世界
万有引力の話
scienceの部屋

平板コンデンサー内部の電界と容量

静電気力も万有引力と同じく、距離の逆2乗に礼する力だ。すなわち、
   　      万有引力；　f＝Gmm'/r²
　    　      クーロン力；f＝kqq'/r²
G→k、m→q、m'→q'とすれば全く同じ式であることが分かる。ただし、質量にはマイナスの値は無いが、電荷は正負の両方の値を取る点だけが異なっている。だから、無限に広がった平面での万有引力に議論がこのまま適用できることになる。
ここに、比例定数kは、真空中では、9×10⁹[Nm²/C²]の値。平板平面コンデンサーの電荷密度をσ[C/m²]としよう。上板は＋、下板は－に帯電している。コンデンサー内部にある＋1Cの単位正電荷に対しては、上板からは2πkσの斥力(同符号)、下板からは2πkσの引力(反対符号)のが働き、結局内部の力は4πkσの下向きの力が働くことになる。この力を電界と称する。この単位正電荷に働く力は無限に広がった平面での万有引力の場合と同じで平板に位置によらず一定というところが大事だ。だから、コンデンサーの外側では、単位正電荷に働く2つの板からの力は打消し合って、コンデンサーの外側の電界は零となる。
実際には、平板は無限の広さを持つわけではないが、極板間の距離に比べて平板が十分に広い場合はこの関係が成り立つと考えられる。
ところで、電位差というのは、力が働いている電界内で、単位電荷を動かすのに必要な仕事のことを言う。だから、極板間の電位差は、極板間の距離をd[m]として,    　      V＝Ed＝4πkσd[V]
電位差の単位はV(ボルト)で表わす。
次に、コンデンサーの極板の面積をS[m²]、蓄えられている電気量をQ[C]とすると、Q＝Sσ、一方電気容量をC、Q＝CVとすると、
   　       C＝Q/V＝Sσ/4πkσd＝(1/4πk)(S/d)となる。これがコンデンサーの容量を表す式だが、この単位をF（ファラッド）と呼ぶ。
電気の場合は、単位が結構分かりにくい。電荷の電気量の単位をC(クーロン)出表すので、クーロン力のfは勿論N(ニュートン)ですが、
係数のkは、[k]＝[Nm²/C²]、[E]＝[4πkσ]＝[N/C]、[V]＝[Ed]＝[Nm/C]、さらに、
[C]＝[Q/V]＝[(1/4πk)(S/d)]＝[C²/Nm]＝[F]、コンデンサーの容量はF(ファラッド)で表す。

物理の世界
万有引力の話
scienceの部屋

運動エネルギーとポテンシャルエネルギー

ニュートン以降の力学の発展の中で、運動の大きさを表す尺度として「運動量mv」と「運動エネルギー(1/2)mv²」のどちらが適切か論争が当時の学者たちの中で闘わされたという。現在ではどちらも運動を表す大切な尺度として定着しているが、性質はずいぶん異なるのでしっかりと使い分けできるようになりたい。
【運動方程式の積分】
質量mの物体が力Fを受けて運動した時、その運動方程式は、
   　      md²x/dt²＝F…(1)となるのが有名な運動方程式。この両辺にdx/dtをかけて、tについて積分する（t＝t₀～t）。
   　      m∫_t0^t(dx/dt)(d²x/dt²dt＝∫_t0^tF(dx/dt)dt
ところが、d/dt(dx/dt)²＝2(dx/dt)(d²/dt²であるから、左辺の積分は、次のようになる。
   　      (m/2)∫_t0^td/dt(dx/dt)²dt＝[(m/2)(dx/dt)²]_t0^t
ここでdx/dt＝v(速度)とすると、上式は、    　      mv²/2－mv₀²/2
右辺については、∫F(dx/dt)dt＝∫Fdxとなる。結局上の積分からは次の方程式を得ることができる。
   　      (mv²/2)－(mv₀²)/2＝∫_x0^xFdx
ここで、mv²/2は運動エネルギーと呼ばれる量で、運動エネルギーの変化が仕事に変換されることを示している。

物理の世界
万有引力の話
scienceの部屋

気体の圧力を統計力学的に求める

気体を剛体の球(気体の分子)が自由に飛び回っている状態と考えます。一辺の長さがL、体積がV＝L³＝L×L×Lの硬い箱の中に、質量mの気体分子がN個含まれていて、ランダムに飛び回っている状況を考えます。これを理想気体とします。重力の影響はここでは無視。気体の分子同士、および気体分子と剛体壁は弾性衝突(反発率 e ＝1)するとします。つまり、衝突の前後でエネルギーが失われることが無い状態です。かなり無理な仮定のように見えますが、簡単なモデルということで案外うまく行くかも。
　さて、図のように箱の辺に沿って座標軸x、y、zを取ります。x軸に垂直な壁S(右側としましょう)が受取る圧力を求めます。y、z軸で考えても同じですね。気体分子は各々勝手な速度で飛び回っていますが、そのうちの1つを取って、その速度をｖ、成分をv_x、v_y、v_zとします。分子が壁Sと衝突すると、
速度はv_xから－v_xに変化。運動量はmv_xから－m v_xに変化します。分子は壁からこれに相当する力積をうけ(x軸の負の方向)、壁はその反作用として反対向き(x軸の正の方向)の力積を受けます。壁が受ける力積は、 m v_x－(－m v_x)＝f △t　(運動量の変化 ＝ 力積)から、
　        f △t＝2 m v_x　　…(1)
△ tは、本来は力の作用時間ですが、反発率1の剛体では△ｔは0、力は無限大。でも、実際にはｆと△ｔの積は有限です。完全剛体自体が一つの理想化したモデルですから、実際の衝突の問題では力積を使わないといけないのです。
△ｔは分子が衝突してから次に衝突するまでの時間を考えて、その間は一定の力がかかっていると考えるます。分子の数がうんと多ければそのように考えてもいいですね。分子が壁に衝突して反射して反対の壁にぶつかりまた反射して壁Sに到達するには距離 2 L 進みます。その間の時間は、       △ t＝2 L/ v_x　となります。これを(1)に入れると、
f＝m v_x² / L …(2) の力を受けることが分かります。 一方、v²＝v_x²＋v_y²＋v_z²
平均を取る操作を{ }で表します。すなわち{v²}＝(1/N)∑ v²、 Nは総ての分子の数。∑の和 i＝1～Nは、自明なので省略。
v_x、v_y、v_zは、個々の分子では色々な大きさがあるが、平均値をとると空間の等方性から同じになります。
つまり、{v_x²}＝{v_y²}＝{v_z²}＝ (1/3) {v²}
N個の分子から壁 S が受ける力Fは f の総和を取り、 F＝∑ (mv_x²/L)＝ m {v_x²} N / L＝ N m{v²}/ (3L)
これより、壁 S が受ける圧力 p は
  　p ＝ F /L² ＝ N m {v²} / (3 L³)＝ N m {v²} / (3 V)　　…(2)
これで、気体分子運動の平均的な速さが分かれば、箱の中の壁に作用する圧力が求められます。
箱の中の気体は方向に関係なく均一な p という圧力が存在しています。ここで、N をN_A (アボガドロ数) とすると、気体の状態方程式から、
  　p V＝ R T＝N_A m {ｖ²} / ( 3V) ×V＝N_A m / 3
  　 m {v²} ＝ 3 R T / N_A
  　(1/2) m {v²}＝ (3/2) (R / N_A)T＝ (3/2) k T
左辺は、分子1個当たりの平均運動エネルギーです。理想気体では平均運動エネルギーは温度だけで決まります。

  　ｋ＝R/ N_Aは、ボルツマン定数と言われるもので　k＝1.38×10^―23J / Kです。
気体全体でのこのエネルギーの総和はは、内部エネルギーと呼ばれます。
  　U ＝ N_A ((1/2) m {ｖ²} )＝(3 / 2) R T　
さらに、1モル当たりの比熱は、温度を1度上げるのに必要な熱だから、
  　C_v＝(3/2) R (T＋1)－(3/2) R T＝(3/2) Rとなる(定積モル比熱)。
【追記】2017.8.28
　気体の圧力は、このように統計的手法でうまく説明できます。しかし、ボルツマンがこれを発表した当時は、全く無視されてします。当時は分子という概念は実体として解明されておらず、圧力は流体力学的な連続体モデルで説明されていました。例えば水を考えると、パスカルの法則に見られるように、圧力は瞬時に伝わる連続体で、ポツポツの粒子が自由に動き回る世界は想像外だったのでしょう。確かに水圧に関してはこのモデルで説明することは難しそうです。

物理の世界
scienceの部屋

静水圧とは

　アリストテレスは、力が物体に作用すると物体は動き(運動し)、力が働かなければものは動かないと考えていた。コップに水を入れておいておけば、水は力が働いていないので動かない。しかし、コップは水が入ったため明らかに重くなっており、それが置いてある机により多くの圧力を与えるだろう。あなたが机を下向きに押せば、力が必要ですが机は動きません。また、あなたがいかに力持ちでもあなたの体重よりも大きな力で下向きに押すことは不可能です。ここで、作用反作用の法則を思い出してください。机が動かないということは、机から上向きの力が働いているのでしたね。動かないということは、力が働いていないのではなく、働いている力が釣り合っているためと分かることは大きな進歩です。
　では、圧力とは何でしょう。簡単に言えば単位面積当たりの力です。あなたが面積Sの板の上に乗り、あなたの体重がM(kg)とすると、その時の圧力P(N／m²)は、
P＝Mg/S　【N／m²】、
gは重力加速度で地上では、9.8m/s²、体重は正確には質量と言わねばなりません。ところがあなたが乗った板には本当に均等な圧力がかかっていたとは言えません。上のPは、平均の圧力です。実際には板の端と真ん中ではちがう圧力でしょう。
　話がそれますが、土木や建築の分野では、出来上がったコンクリートの強度を確認するために、現物と同じ条件で試験練(ねり)で拵(こしら)えた円柱の供試体を何本も造り、これを機械的に潰してどこまで耐えられるか試験します。この試験体をつくる円柱の大きさ等の仕様はキチンと決まっていて、これ以外は認められません。供試体の大きさが変わると強度が異なってしまいます。所要のコンクリート強度を確保するためには結構色々な条件を考慮する必要があるのです。強度というのはコンクリートの内部に発生する圧力に対する耐久力です。コンクリートの年齢(打設してからの時間経過)、配合(水、砂、砂利、セメントの量と割合)、温度等色々考慮する必要がありますが、円柱の大きさが決まっている最大の理由は、コンクリートの場合、内部の圧力の分布は均一にはならないためです。供試体が大きい方が耐久力があるようです。
この点、水(流体)を対象にすると圧力はずっと簡単になります。水圧は、流体の中に仮想の面を考えると面がどちらに向いていても面に垂直な成分しかありません。上で述べたコンクリートのように面の向きで圧力の値が異なったり、面に平行な成分が発生するものを応力と称しています。詳しくは、材料力学等の分野を学ぶ必要があります。
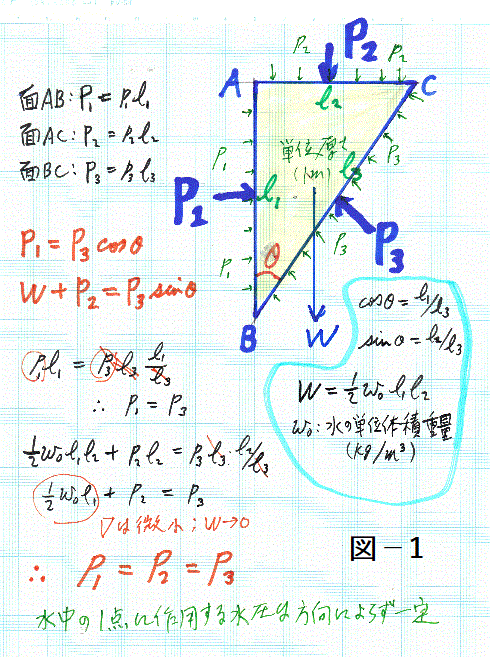
【水中の一点に作用する水圧は、その方向にかかわらず強さが等しい】
図1に示すように、一辺が鉛直な三角形の単位長さの仮想三角柱が水中にあるとします。この三角柱に作用する力は下向きの重力だけです。
結局水中の圧力は、深さが一定ならどの方向でも一定になります。材料が固体(剛体ではない)ではこうならず、応力テンソルという物理量が必要になります。
次に、水中で仮想の鉛直筒体を考え、切り口を単位面積とすると、w₀は水の単位体積重量(ρg)だから、
       p₂＝p₁＋w₀H、ここでw₀は水の単位体積重量(ρg)だから、
       p₂－p₁＝w₀H
また、右図では、p＝p₃－p₀＝w₀H、p₀は大気圧。大気圧を零(基準)と考えて、p/w₀＝Hを水頭(head)と言います。
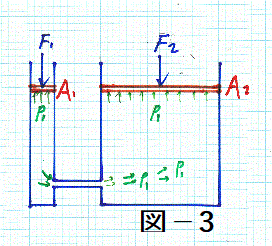結局静水圧とは深さだけの問題ですね。次に示すのはパスカルの原理とも言われているもので、「密閉容器中の流体は、その容器の形に関係なく、ある一点に受けた圧力(単位面積当たりの力)をそのままの強さで、流体の他のすべての部分に伝える。」 というもの。建設機械等に使われる油圧の原理もこれですね。
油圧ポンプの原理です。左側のピストンをF₁の力で押すと、水圧はp₁＝F₁/A₁となります。右側のピストンは断面積をA₂とします。例えばA₂/A₁＝100とします。p₁はパスカルの原理で右側に伝わり、右側のピストン内の圧力はp₁です。だから、右側のピストンに作用する圧力は、F₂＝p₁A₂＝(F₁/A₁)A₂＝F₁(A₂/A₁)＝100F₁となります。力が100倍に拡大されます。もちろん左側のピストンは100倍の距離を動かさなければいけませんが。建設機械は大きな力を出しますが、決して電源コードを引きずっていませんね。油圧を使うと大きな力を発揮することが出きる訳です。

物理の世界
scienceの部屋

気体の状態方程式

気体というものは、身の回りにありながらその存在が本当に分かりにくい。そもそも見ることが出来ない。液体なら、暖めても体積は変わらない(本当は変わるのだけどたいてい無視できる)のに、気体の体積は簡単には測れない。熱機関等の発達で水蒸気等を取り扱い始めてようやくその物理的な性質を記述できるようになります。
最初に出て来るのがボイルの法則(1662年)、続いてシャルルの法則(1787年)が発見されて気体の性質が調べられるようになります。これらは1つにまとめてボイル・シャルルの法則と呼ばれます。かなりの昔のことだ。
気体の状態は、結局f (p,V,T)＝0という形で表せます。つまり、圧力p、体積V、温度Tの3つの状態量のうち2つを決めると後の一つは自動的に決まってしまう。でもどれか一つだけ動かすことは難しい。
ボイル・シャルルの法則は次の(1)式の簡単な形で表わされます。この式が成り立つような気体を理想気体と言います。気体の性質をうまくモデル化したわけです。
      ボイル・シャル法則：　pV＝nRT…(1)
nは気体のモル数です。圧力pはPa(パスカル)＝N/m²、体積Vはm³、温度Ｔは絶対温度Kとすると、R＝8.3 J/mol-K、これを気体定数と言います。絶対温度は摂氏℃の温度に273.15を足したもので、絶対温度を使うと（1）式のように圧力、体積と温度が比例関係で表せます。つまり、体積∝温度、圧力∝温度、体積∝1/圧力の便利な関係が得られます。ただし、変数が3つなのでどれか一つを固定して考えないと難しい。だから偏微分が沢山出て来る。慣れれば普通の常微分と同じですが。
それと、(1)から分かるように、温度は上限が無いですが下限は存在します。T＝0Kになると、体積か圧力のいずれかが0になってしまいます。実際には空気は液化してしまいます。

ボイル・シャルルの法則が成り立つ気体を理想気体といいます。常温で普通の気体を扱っている時は、理想気体はかなり良い近似(ボイル・シャルルの時代はこれで充分だったのでしょう)とされていますが、実在の気体を取り扱うためボイルシャルルの法則とはかなり異なった形の状態方程式       　f ( p, V, T )＝0も提案されています。

理想気体の内部エネルギーについては箱の中を自由に飛び回る、N 個の剛体粒子モデルで既に求めました。統計力学的な手法です。でも、このような離散化したモデルは当時の学会ではなかなか受け入れてはもらえなかったようです。空気も水と同じで連続体として考えたいですから。そもそも分子や原子の存在等当時知られていたはずもなかったですから。理想気体の内部エネルギーを連続体のモデルで導くにはどうすれば良いのでしょうか。
気体の圧力を統計力学的に求める
その結果(統計力学的の求めた結果)、空気分子の力学的運動エネルギーの総和 Ｅ( 1 モルの場合)が
       E＝∑(1/2) mv(i)² ＝ (3/2) R T…(3)
となることが分かります。理想気体では飛び回る空気分子の運動エネルギーの総和を内部エネルギーと定義するのです。また、これが温度の正体ともいえるのですね。また、 p V＝ R T の関係があるので
       E＝ (3/2) p V、すなわち　
       p V ＝(2/3) E
　これをベルヌーイの関係と称している。
一方、実在の気体を取り扱うための状態方程式として良く使われるものに、ファン・デル・ワールス(van der Waals)のものが良く使われている。
      ( p＋a/V² ) (V－b) ＝ R T
ここで、 a、 bは気体毎に異なる物質定数です。

【気体の圧縮率・膨張率】
気体は温度や圧力の変化で体積を大きく変えるのが特徴です。その基本的な性質、気体の膨張率と圧縮率を求めましょう。
右記の通りです。
温度を上げると気体は膨張します。この時は圧力を一定にしておきます。これが(定圧)膨張率。また、気体を圧縮していくと縮みます。この時は温度を一定にしておきます。これが(等温)圧縮率です。圧縮率の方は圧力が増えると体積は減るのでマイナスの符号を付けます。
p、V、Tの三つの変数は互いに関連し合うので、どれか一つを一定にしておかないとややこしいですね。なお、理想気体については、膨張率はβ＝1/Ｔ(定圧)、圧縮率はκ＝1/p　となります。
何故ならば、理想気体では常に p V ＝ R T の関係があります。従って、
       β＝(1 / V)(∂V/∂T)_p ＝(1 / V)∂/∂T (RT/p)_p ＝(p / R T)∂/∂T (R / p)_p＝ 1 / T
       κ＝(－1 / V)(∂V/∂p)_T ＝－(p / R T)∂/∂p ( R T / p)＝－(p / R T)(－R T / p²) ＝ 1 /p
      　(∂p/∂T)_V＝∂/∂T( R T / V)_V＝ R / V ＝ R p / R T＝ p /T ＝ β/κ
と右の関係は簡単に求まります。
【偏微分の公式】
なお、F( x, y, z )＝0 の時に、(∂z/∂x)_y(∂x/∂y)_z(∂y/∂z)_x＝－1　という関係が知られています。
気体の体積をV＝V( T, p )とすると、
       dV＝(∂V/∂T)_p dT＋(∂V/∂p)_T dp
      dV/V＝(1/V) (∂V/∂T)_p dT＋(1/V) (∂V/∂p)_T dp＝βdT－κdp　…(4)
となります。
第一項が温度上昇による体積の増加率、第二項が温度が一定の場合の圧力増加に伴う体積の収縮率です。つまり気体の体積が変化する原因には温度が上がる/下がる（膨張/圧縮）か圧力が増加/減少する(圧縮/膨張)かの2つの要因があります。

理想気体の場合は、 β＝1/T、κ＝1/p だから、(4)は、
      dV/V＝dT/T－dp/p、すなわち ∫dV/V＝∫dT/T－∫dp/p
積分範囲を(V₁, p₁, T₁)→(V₂, p₂, T₂)とすると、
       log(V₂/V₁)＝log(T₂/T₁) －log(p₂/p₁)
       ∴log( V₂/V₁・ p₂/p₁・ T₁/T₂ )＝log(R T₂/R T₁・T₁/T₂)＝log 1＝0
ここでは、pV＝RTの関係を使っている。
これは一体どういう意味なんでしょう？？



【対数計算のコメント】
ところで、対数関数の積や商は、高校の数学では和や差で表されると習ったはず。
log ab＝log a＋log b、log a/b＝ log a－log b
しかし、logの中は当然無次元です。logの中が、温度や体積、圧力になるのは大変可笑しい。。指数関数や三角関数でもそうですが、上の場合は特にうっかりしやすいと思います。ただ、熱力学の教科書では、log(p)やlog(V)が平気で出て来ます。たいていは、和とか差を取ると無次元のなるので問題はないのですが気になる所です。
ある数を〇乗したら、M(任意の数)になるとします。この時、
a^x＝Mですが、これをx＝log_aMと表します。aは対数の底と言います。
例えば、常用対数は底が10で、2＝10^x、x＝log₁₀2＝0.301だから、2＝10^0.301
2¹⁰⁰＝(10^0.301)¹⁰⁰＝10^30.1＝10³⁰×10^0.1＝1.259×10³⁰　(10^0.1＝1.259)
    大きな数を扱う時には対数は大変便利です。ところで、自然科学の分野で対数を利用する時は、ほとんど底はe(＝2,718---)を用います。
e^x＝y　の逆関数がx＝log yです。ここで注意してほしいのは、xは普通の数ですね。つまり無次元数。e^x-kg、 e^x-m 、e^x-Pa 等ということ絶対ありえないですね。ということはｙも無次元でないとおかしいですね。
y＝Ae^xとすればyはAと同じ次元です。Aに単位が入っていても問題ないね。
両辺の対数を取れば,
log y＝log A＋x、x＝log y－log A＝log(y/A)
この時、上の式のlog y、log Aは、本当はおかしいでしょう。log(3kg)なんてある訳ないから。最終結果はＯＫでしょうが。積分の時もあります。
∫dx/x＝log|x|＋C、xが圧力とか単位を持っていたら、左辺は無次元ですが、右辺のlogの中には単位が入って来てしまいますね。積分定数がついているのでうまく調整は聞くのですが、なんとなく感じが良くないですね。

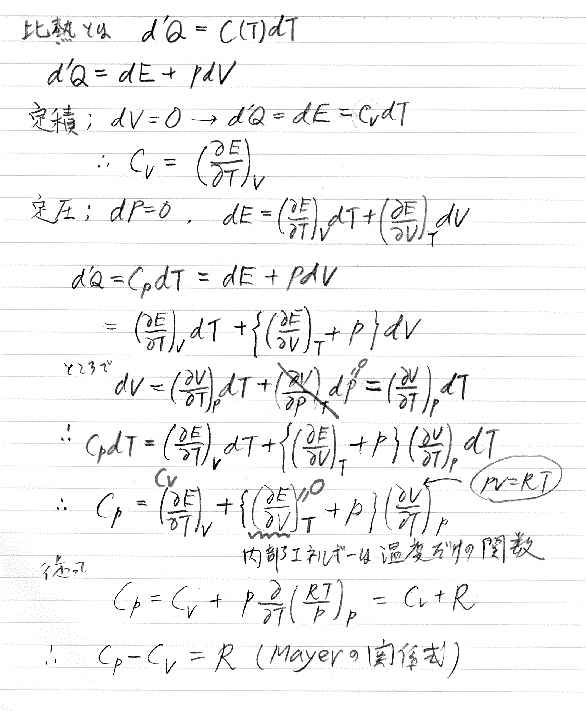【気体の比熱】
次に気体の大事な性質は比熱でしょう。温度を1K上昇させるのに必要な熱量（エネルギー）です。比熱が大きいということは温まりにくく冷えにくいということ。比熱の大きなものの代表は水です。空気の場合は、熱すると膨張しようとします。水は熱してもほんの少ししか膨張しません。だから、空気の比熱は定積比熱と定圧比熱の2つを考えないといけません。密閉容器の中で熱した場合と大気圧状態で熱した場合です。これが定積比熱と定圧比熱です。当然定積比熱の方が小さいはずです。定圧の場合、膨張するという仕事にエネルギーが使われてしまいますから。
比熱は温度の関数です。つまり、d'Q ＝ C(T) dT
気体に熱を加えると、一部は膨張という仕事に使われ、別の部分は内部エネルギーの増加に使われます。すなわち、d'Q ＝ dE＋ p dV…(1)となります。
定積の場合は　dV＝0　ですから、d'Q＝dE=C_vdT となります。すなわち、C_v＝dE/dT　としたいところ、これでは体積が一定ということが分かりません。だから C_v ＝(∂E/∂T )_V　と表わします。熱力学でやたらと偏微分が出て来るのはこのような訳があります。

次に、定圧の場合は、　dE ＝(∂E/∂T)_V dT＋(∂E/∂V)_T dV
(1)式から、d'Q＝C_p dT＝ dE＋p dV＝(∂E/∂T)_V dT＋(∂E/∂V)_T dV＋p dV＝(∂E/∂T)_VdT＋｛(∂E/∂V)_T＋p｝dV
ところで、dV＝(∂V/∂T)_p dT＋（∂V/∂p）_Tdp＝(∂V/∂T)_p dT 　　 (∵dp＝0；定圧)とできるので、
C_pdT＝dE＋pdV＝(∂E/∂T)_VdT＋｛(∂E/∂V)_T＋p｝(∂V/∂T)_pdT
C_p＝(∂E/∂T)_V＋｛(∂E/∂V)_T＋p｝(∂V/∂T)_p
∴C_p＝C_V＋p(∂V/∂T)_p　…(4)
(4)では、C_V＝(∂E/∂T)_V、(∂E/∂V)_T＝0 (内部エネルギーは温度だけの関数)の関係を利用しました。
PV=RTの関係から、p(∂V/∂T)_p＝p∂/∂T(RT/p)_p＝R　だから、
  　C_p＝C_V＋R
これはMayerの関係式と言われ、定圧比熱と定積比熱の差は気体定数の差となります。
自由に分子が飛び回る理想気体の内部エネルギーは次のようになることが知られています。
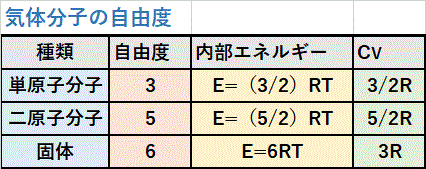気体分子には自由度があって、内部エネルギーはその各々の自由度に均等に配分されるという法則があります。例えばヘリウムのような単原子分子の自由度は x, y, z で自由度 3 ですが、固体や3(以上)原子ではそれに x, y, z 軸回りの回転が加わり自由度は 6 になります。その結果、内部エネルギーと定積比熱は自由度の応じて表のように。閉じ込められた気体に加えられた熱は、総て内部エネルギーの増加になります。対応する定圧比熱はMayerの関係式から求めることが出来ます。
先に示した、E＝(3/2) R T は単原子分子の場合、この時はC_v ＝(∂E/∂T )_V＝(3/2) R　となりますが、H₂、O₂は2原子分子なので、C_v ＝(5/2) R 、C_P＝C_v＋ R ＝ (7/2) R となります。

物理の世界
scienceの部屋

熱力学とエントロピー

目次 　　

エントロピーとは何だろう＝エントロピー増大の法則	エントロピーを計算して見る	等温変化と断熱変化
カルノーサイクル	情報工学とエントロピー

エントロピーとは何だろう＝エントロピー増大の法則

エントロピーという言葉は、最近良く使われるようになって来ています。本来は、物理学の中の熱力学という分野で使われ始めたのですが、それが統計力学の確率的な見方を通して、分子運動の乱雑さを表す指標と同じものであることが分かります。それが情報の不確実さを表す指標と同じものであることが、明らかになり情報工学分野でも盛んに使われるようになってきました。また、環境問題でも環境の質を評価する一つの指標としても使われるようになってきています。
    エントロピーは、エネルギーと並んで自然を理解する上で非常に重要な概念です。ただ、力や加速度、距離や時間と異なり直感的に理解するのが難しいので基礎的な考えを学んでおくことが必要なようです。まず、熱という量は結構分かりにくい所があります。病気になって熱がある。熱はある訳はない。体温計で計るのは体温つまり温度です。熱とはエネルギーの流れで、直接は計ることが出来ない量なのです。このような量としては、力学で使う仕事という概念も同じです。仕事も力×動いた距離、Ｗ＝Fdで力の流れみたいなもの。そういえば、熱力学でd’Qとかd’Wとかあって、これは全微分ではないですよ。普通の微分ではない単なる微小量ですとよと教わった記憶があります。さらに、熱も仕事もエネルギーの単位J(ジュール)で計測されます。つまり、熱と仕事を組込んでエネルギーの保存則が成り立っている訳です。熱はエネルギーの一形態であり、熱を利用して色々な機械を動かして仕事をすることができます。しかし、熱エネルギーはどんなに頑張ってもすべてを仕事に変えることは出来ません。
   このことを最初に研究したのが、カルノーサイクルで有名なサディ・カルノー(1796～1832)です。熱機関というものは、結局高温の熱源T_Hからエネルギーを受取り仕事をして低温熱源Ｔ_Ｌに熱を与えてもとに戻るサイクルを繰返して動きます。最も効率の良い理想的なサイクルを考えてもその効率は限度があります。熱エネルギーは大抵の場合、半分以上は捨てざるを得ない宿命があります。蒸気機関車はせいぜい10～15%程度の効率、火力発電でも40％を越えれば上出来です。それでは、どうして火力発電を止めて水力に変えないのか。水力発電ならエネルギー効率は90％以上も可能なのに。ところが化石燃料には古代の生物達が貯金してきた膨大なエネルギーがコンパクトに蓄えられています。水力を使うには大規模な土木工事が必要で環境への影響も小さくありません。経済効率からは圧倒的に化石燃料は有利です。ただし、近年は地球温暖化と資源の枯渇の問題から化石燃料を多量に消費することは問題がありますが、エントロピーとは直接関係ななさそうです。
   熱とは結局、高温から低温に流れるもので、その逆はありません。そして、この時必ず増えていくのがエントロピーという物理量です。このような変化を不可逆変化と言います。コップに落としたインクがコップ全体に広がってしまって元に戻らないのが不可逆変化。情報の世界では噂が広がって尾ひれがいっぱいついて元の情報が分からなくなってしまうのも不可逆変化。情報の不確かさを表すのもエントロピーと言う指標を使います。
　森羅万象色々な人や自然の活動の結果、最後に残るのは低温の熱源だけ、エントロピーはどんどん増大していきます。世界(宇宙)は、最後には一様な低熱源のみの死の世界。これを「熱的死」というのだそうです。運動量やエネルギーの保存則と比べてあまり明るい感じの法則ではないでしょう。色々なシステム(環境や社会的システムも含む)にとっては、自己のシステム内のエントロピーを以下にいかに増やさないようにできるか大変重要な問題となって来ているのです。

熱力学とエントロピー
物理の世界

エントロピーを計算して見る

熱力学でのエントロピーの定義は極めて単純です。       dS＝d’Q/T……(1)
エントロピーの単位は、エネルギー（熱）を絶対温度で割ったもの、つまり、同じエネルギーでもその時の温度によって価値が違うぞと言っているんです。移動した熱量をその時の絶対温度で割るだけです。
d’Qとダッシュがついているのは、熱量の移動は全微分にならないからですが、Tで割った結果のdSは全微分になるのはチョット不思議な気もしますが。全微分にならないと熱の移動の仕方でその都度その量が変わるので微分積分など操作に耐えられないという問題があるんです。
       △S＝△Q/T……(2)
と書いてある教科書もあるかもしれないが、系の温度が変化する場合は、(1)の表示は不正確だし、(2)では足し合わせて積分するにも不便です。
ただし、系の温度が変化しない場合には、(2)を使うことが可能で、そのような特例として(水の)融解と蒸発の例があります。

なお、以下の問題では、熱量の単位 cal を SI 単位に直す必要があります。仕事やエネルギーの単位はJ(ジュール)です。換算係数は 4.1855 J/cal です。
【問題1】1気圧のもとで、０℃、1gの氷がとける時のエントロピーの増加量
水の融解の潜熱は80cal/gでした。０℃＝273K     △S＝△Q/T＝80/273＝0.29[cal/K・g]＝1.23[J/K・g]
　氷が融解して水になるとエントロピーが増加します。

【問題2】1気圧のもとで、100℃、1gの水が蒸発する時のエントロピーの増加量
水の蒸発の潜熱は540cal/gでした。100℃＝373K     △S＝△Q/T＝540/373＝1.45[cal/K・g]＝6.06[J/K・g]
　水が蒸発して水蒸気になるとエントロピーが増加します。

【問題3】理想気体の場合…1モルの理想気体を考えて、その温度や圧力が変化した時のエントロピーの増減を考えてみます。
　１モルの理想気体(これを系とする)を考えます。理想気体では、状態方程式  pV＝RTが成立します。その時、
①体積が一定で、温度がT₁からT₂に増える時の系のエントロピーの変化
②温度が一定で、体積が体積がV₁からV₂に増える時の系のエントロピーの変化
③体積が一定で、圧力がp₁からp₂に増える時の系のエントロピーの変化
④体積が一定で、圧力がp₁からp₂に増える時の系のエントロピーの変化
となる場合の変化を求めてみます。まず、熱力学の第一法則を最初に考えないといけません。
      d’Q＝dU＋pdV……(3)
この式の意味は、熱が与えられれば、それは内部エネルギーの増加（温度が上がる）に使われるか、或いは圧力が増えて体積の増加に使われるか、その両方かのどれかで、エネルギーの保存則を示しているのです。
①では体積が一定で、温度がT₁からT₂に増える時の系のエントロピーの変化です。体積一定ですから、(3)式のpdV＝0です。理想気体では内部エネルギーUは温度のみの関数ですから、d’Q＝dU＝CvdT(モル比熱に温度上昇を掛けたもの。これが定積比熱の定義。)
       ∴dS＝d’Q/T＝(Cv/T)dT、            ∴△S＝Cv∫_T1^T2(dT/T)＝Cvlog(T₂/T₁)　(体積が一定)……(4)
(T₂＞T₁)だから、温度が上がればエントロピーは増大します。

②では温度が一定で、体積がV₁からV₂に増える時の系のエントロピーの変化です。温度のみに依存する内部エネルギーの変化は0、すなわちdU＝0です。
従って、dS＝d’Q/T＝(p/T)dV、    ∴△S＝∫_V1^V2(p/T)dV＝∫_V1^V2(R/V)dV＝Rlog(V₂/V₁)(温度が一定)……(5)
V₂＞V₁だから、体積が増えてエントロピーは増大します。

③では、体積が一定で圧力がp₁からp₂増加する場合だ。
　p V＝ R T の関係を用いると、体積が一定で、圧力がp₁からp₂に増えるということは温度がT₁からT₂に増えることと同じだ。この時の系のエントロピーの変化は(4)から、
  　△S＝Cv log(T₂/T₁) ＝Cvlog (p₂/p₁)
この場合も熱が与えれれ圧力が増加してばエントロピーは増えるんですね。

④最後に温度が一定で、圧力がp₁からp₂に増える時の系のエントロピーの変化は、体積が V₁から V₂に減少することと同じだ。
    △S＝Rlog(V₂/V₁) ＝Rlog(p₁/p₂)
この場合は、圧力が増えると、体積は減少するのでエントロピーは減少する。

【多項式の積分】
なお、積分計算では、一般の多項式では
    ∫xⁿdx＝(１/(n＋1))x^(n＋1)＋C
    ∫x ^-mdx＝(１/(-m＋1))x^(-m＋1)＋C
が、一般に成り立つのですが、n＝－１( m＝1)の時に限って、
   ∫ x^-1 dx＝∫ dx / x＝log|x|＋C

となる。熱力学でやたらとlogが出て来るのはpとVが反比例の関係があるため。

熱力学とエントロピー
物理の世界
scienceの部屋

情報工学とエントロピー

情報は確実性が命、エントロピーは少ないほど良い。情報は多い方が良いという思い込みはここでは捨てなければならない。エントロピーは不確実性の尺度です。
まず、簡単な例をあげてエントロピーSを求める。
〇カードが沢山あっても同じもので選択の余地がない場合。S＝0
〇2種類のカードが同数ある。二者択一の場合。S＝1
〇4枚の異なったカードから1枚をあてる。S＝2
〇8枚の異なったカードから1枚をあてる。S＝3
〇16枚の異なったカードから1枚をあてる。S＝4
エントロピーは、S＝log₂Nとなりそうだ。
これを、もっと一般の場合に適用できるようにしたのが、
S＝－∑i(Pi) log₂ Pi …(1)
もう少し、例題をやって見ましょう。 〇3枚の異なったカードから1枚の正解を見つける。
S＝－3×(1/3) log₂ (1/3)＝log₂ 3＝log₁₀ 3/ log₁₀ 2＝1.585
〇将棋の金4枚をふる。場合の数は全部で16通り(24)ある。
表を1、裏を0として、その合計を求める。
0…0000→1通り、1…0001、0010、0100、0100→4通り、
2…0011、0101、0110、1001、1010、1100→6通り(₄C₂＝6),
3…0111、1011、1101、1100→4通り(₄C₃＝4)、4…1111→1通り
全部で1＋4＋6＋4＋1＝16通り、従ってエントロピーSは、
S＝－｛2×(1/16)×log₂(1/16)＋2×(4/16)×log₂(4/16)＋1×(6/16)×log₂ (6/16)) ｝
      ＝2.031
情報工学の場合は、Sを情報のビット数と考えることもできる。一般の統計力学の場合、対数の底は2ではなく。eを用い、場合の数はものすごく多い(例えばアボガドロ数6×10²³個)ところが異なっている。

熱力学とエントロピー
物理の世界
scienceの部屋

等温変化と断熱変化

エントロピーの熱力学的な説明を解明するために、まず始めに有名なカルノーサイクルの説明を行ってみたい。まず、その準備として気体の体積変化にかかわる、等温変化と断熱変化について考察する。体積変化には圧縮と膨張がある。外から仕事をもらうのが圧縮、外へ仕事をするのが膨張である。熱も仕事もエネルギーそのものではなく、系(シリンダー)に出入りする量でエネルギーと同じ単位(J)で表される。カルノーサイクルは等温変化と断熱変化を組合わせて造った単純化された仮想的なサイクルで熱機関の本質を見事に解明することに成功している。
【等温変化】
シリンダーを熱源(高温と低温の2種)に接触させて、温度が一定の条件での圧縮及び膨張を行う。「気体の圧力を統計力学的に求める」の項で考察したとおり、気体の内部エネルギーは温度だけで求まるという性質があります。ここで気体は理想気体を対象としていますが、実際の大気も幸い普通取り扱われる温度では理想気体に近い挙動を示すと言われています。
この時、圧力と体積には、
pV＝(2/3)U＝ｎRT＝NkT…(1)という関係が成立します。
ここでUは内部エネルギーと呼ばれる量で、気体分子の平均エネルギーの総和となっています。従って、ここでは温度が一定なのでボイルの法則が成立します。
【断熱変化】
シリンダーを熱源から切り離し、熱の出入りの無い状態で圧縮及び膨張を行います。この時ピストンの行う仕事は、
△W＝F△l＝pA△l＝p△V (lは小文字のエルです。また、A△l＝△V。)
また、U＝(3/2)pVから、U＋△U＝(3/2)(p＋△p)(V＋△V)…(2)
　　　△U＝－△W＝－p△V(仕事をすれば内部エネルギーは減り仕事を受ければ増える)
であるから、(2)式は
　　 (3/2)pV－p△V＝(3/2)(pV＋p△V＋V△p＋△P△V)(最後の項は微小)
これをまとめると、　－5 p△V＝3 V△p→微分に直す
　　　dV/V＝(－5/3)dp/p
∫dV/V＝(－5/3) ∫dp/pとなるので、log p＝－log V(5/3)
すなわち、　pV^γ＝C(定数)…(3)、ただしγ＝5/3とした。
また、上式にpV＝NkTを代入すると、
　　NkTV^γ－1＝C →∴　TV^γ－1＝C’(定数)…(4)
断熱変化の際のp、Vの関係を別途誘導してあります。

熱力学とエントロピー
物理の世界
scienceの部屋

カルノーサイクル

カルノー(Sadi Carnot、1796年パリ～ 1832年)は、熱機関の効率について画期的な発想で答えを見出した。もともとの出発点は一体熱エネルギーの何割までが仕事に変換できるのかということです。熱機関の複雑な要素を一切取り除き、温度がT_Hの高温熱源と温度がT_Lの低温熱源を用意し、理想気体を詰めたシリンダーを外側から暖めたり冷やしたりするサイクルを考えたのです。また、この過程には、
(1)シリンダーが熱源に接した、温度が一定のままでの膨張と収縮
　→ボイル・シャルルの法則pV=nRTが成立する等温膨張・等温収縮
(2)シリンダーが熱源から切り離された状態での膨張と収縮
　→pV^γ＝C(一定)、TV^(γ－1)＝C’(一定)　(ポアソン公式)の成り立つ膨張と収縮
　　ただし、γ＝5/3、γ－1＝2/3、γ/(γ－1)＝5/2
の組合せの４工程で成立する仮想の熱機関の思考モデルを構築しました。このモデルの概要は下図に示す通りですが、ここでの運動はすべて可逆過程であり得られる効率はT_H、 T_Lを与えた時に得られる最大の効率となっているのが味噌です。可逆過程であっても熱エネルギーはすべてを仕事に変換することが不可能なことがこのモデルから示されます。


【step 1.初めの状態】
　どこからスタートしても良いのでしょうが、まず始めにシリンダーが低温熱源に接していて、シリンダー内部に理想気体が詰まっている。その時の温度、体積、圧力は、
T_L＝0℃＝273K、V₀＝1m³、p₀＝1atm＝1.013×10⁵Pa
状態方程式は、p₀V₀＝nRT_L から
n＝(p₀V₀)/( RT_L)＝1.013×10⁵×1/(8.3×273)＝44.7mol (R＝8.3J/molK)　としましょう。
【step 1.等温圧縮】
　シリンダーが低温熱源に接したまま(温度がT_L)、体積をV₁まで圧縮する。V₁＝0.5ｍ³とします。
ボイルの法則より、p₀V₀＝p₁V₁、すなわちp₁＝p₀×(V₀/V₁)＝2.026×10⁵Pa
【step 2.断熱圧縮】
　シリンダーを熱源から切り離し(断熱状態)、温度がT_Hになるまでさらにゆっくり圧縮する。温度T_H＝100℃＝373Kとする。圧縮後の体積をV₂とする。
      T_LV₁^(γ－1)＝T_HＶ₂^(γ－1)
      →V₂＝V₁(T_Ｌ/T_H)^1/(γ－1)
      ＝0.5×(273/373)^(1/(2/3))＝0.313ｍ³
      従って、p₂＝2.026×10⁵×(373/273)^5/2＝4.42×10⁵Pa　
      (∵γ/(γ－1)＝(5/3)/(2/3)＝5/2)
【step 3.等温膨張】
　シリンダーを高温熱源に接触させた状態で(等温変化)、体積をV₃まで膨張させる。
この時は、ボイル・シャルルの法則から、p₂V₂/T_L＝p₃V₃/T_L　が成り立つが、V₂、p₂ともに未知数ではどこまで膨張させればよいか分からない。しかし、このサイクルは次の断熱サイクルで閉じなければならないので、初期状態V₀、p₀からサイクルを逆回りしてV₃、p₃を求めて見る。
      p₀V₀^γ＝p₃V₃^γ、T_LV₀^γ－1＝T_HV3^γ－1
      V₃＝V₀(T_L/T_H) ^1/(γ－1)＝1×(273/373)^(3/2)＝0.626m³
      p₃＝p₀(V₀/V₃)^γ＝p₀((T_H/T_L) ^1/(γ－1))^γ＝p₀(T_H/T_L)^γ/(γ－1)
      ＝1.013×10⁵×(373/273)^5/2＝2.21×10⁵Pa
【step 4.断熱膨張】
　シリンダーを高温熱源から切り離し、温度がT_Lになるまでゆっくり膨張させる。その結果、状態は体積V₀、圧力p₀の初期状態に戻る。以上でサイクルが一回りするが、その前にstep.3で上で逆算で求めたp₃、V₃がボイル・シャルルの法則を満たしているがチェックしておく必要がある。p₂V₂＝p₃V₃　であるから、
      p₃V₃＝p₀((T_H/T_L)^γ/(γ－1)×V₀(T_L/T_H) ^1/(γ－1)＝p₀V₀(T_H/T_L)
      p₂V₂＝p₁(T_H/T_L)^γ/(γ－1)×V₁(T_L/T_H)^1/(γ－1)＝p₁Ｖ₁ (T_H/T_L)＝p₀V₀(T_H/T_L)(∵p₀Ｖ₀＝p₁Ｖ₁)
すなわち、サイクルは閉じることになり無事モデルは完成しました。上の数値例を下に示します。

po	1atm	V0	1m3
p1	2atm	V1	0.5m3
p2	4.31atm	V2	0.313m3
p3	2.18atm	V3	0.626m3
p0	1atm	V0	1m3

      さて、もう一度カルノーサイクルのポイントを整理します。まず、理想気体を扱っているので、内部エネルギーが温度に比例しているという関係が重要で、
U＝(3/2)pV＝(3/2)NｋTが成立します。
      まず、カルノーサイクルでは、断熱圧縮と断熱膨張の2つの断熱変化があります。最初の断熱圧縮では、(3/2)Nk(T_H－T_L)だけ、シリンダー内の内部エネルギーは増加しますが、断熱膨張の過程で(3/2)Nk(T_L－T_H)だけ失うのでキャンセルされて内部エネルギーは増減なし。断熱過程では、熱の出入りがないので内部エネルギーの増減はすべてピストンの出入りに使われてサイクルの仕事としてはキャンセルされてしまう。
      一方、断熱膨張(圧縮)の関係式は、T_HV₂^γ－1＝T_LV₁^γ－1、T_HV₃^γ－1＝T_LV₀^γ－1
から、この2式の両辺を割り算することで、V₃/V₂＝V₀/V₁が得られる。
と言う訳で、エンジン出力として取り出せる仕事Wは、等温圧縮と等温膨張の2つの過程を比べれば良いことになる。
△W＝p△V(これはV₀→V₁)→W_L＝∫dW＝∫pdV＝p₀V₀∫dV/V＝p₀V₀log(V₁/V₀)
一方、W_H＝p₂V₂log(V₃/V₂) WL＝NkT_Llog(V₁/V₀)＝－NkT_Llog(V₀/V₁)＝－(T_L/TH)Nk T_H log(V₃/V₂)＝－(T_L/T_H) W_H これより、
Q_H/T_H＝W_H/T_H＝－W_L/T_L＝－_L/T_L カルノーサイクルは一巡する間に高温熱源からQ_Hの熱エネルギーを受取り、低温熱源にQ_L＝(T_L/T_H) Q_Hを低温熱源に渡す。差引勘定をすると、 W＝W_H＋W_L＝(1－T_L/T_H) Q_H エンジンが出力として取り出せる割合を熱効率ηと呼ぶが、 η＝W/ Q_H＝(W_H＋W_L)/ Q_H＝(Q_H＋Q_L)/ Q_H＝1－T_L/T_H つまり気体は低温熱源にQ_L＝W_Lの熱エネルギーを渡し、高温熱源からQ_H＝W_Hの熱エネルギーを受取る。最終的に熱効率ηは高温と低温の熱源の温度比だけで決まってしまう。Q_Lは使われることのない熱量なので排熱と呼ばれるが、T_L＝0(絶対温度0)ならば効率は1になることに注目したい。

カルノーサイクルをもう一度示します。



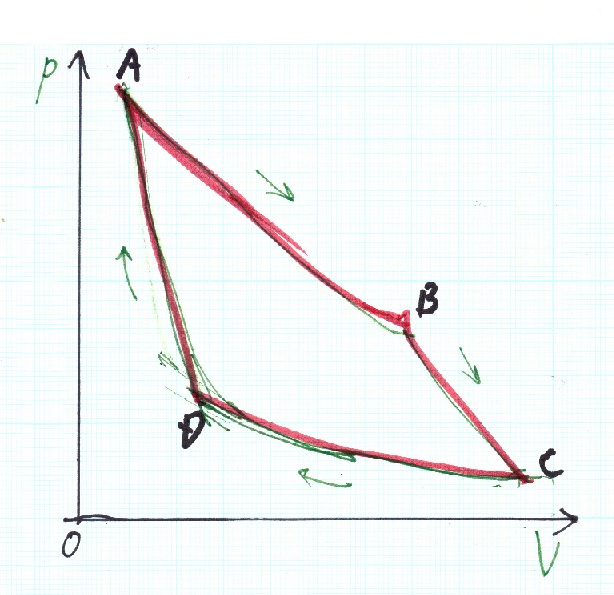
カルノーサイクルでは、結局(V_A/V_B)＝(V_D/V_C)となるので、得られる仕事は、
W_{A→B→C→D}＝W＝R(T₁－T₂)log(V_B/V_A)となります。従って、
Q_A→B：Q_C→D：W＝T₂：T₁：(T₂－T₁)
熱効率を
η＝W/Q＝(Q₂－Q₁)/Q₂＝(T₂－T₁)/ T₂
温度比だけで、効率が決まってしまうのです。
カルノーサイクルの図はp-V図で見るとあまり綺麗ではないけれど、T-S図に表すときれいな長方形になります。ここで囲まれた長方形の面積は、
(S_B－S_A)(T₂－T₁)＝△S(T₂－T₁)＝Q₂－Q₁＝W
で丁度行われた仕事を表しています。エントロピーは一回りすると元に戻ることになりますが、高熱源を冷やしたり、低熱源に熱を与えたりして周囲の環境のエントロピーを増大されているのです。

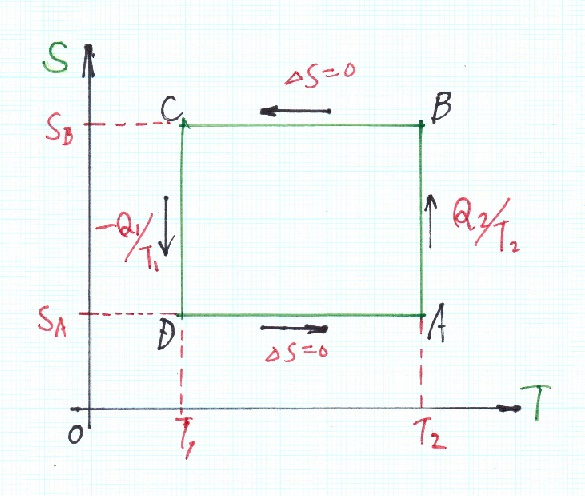
ここで囲まれた長方形の面積は、
(S_B－S_A)(T₂－T₁)＝△S(T₂－T₁)＝Q₂－Q₁＝W
で丁度行われた仕事を表しています。エントロピーは一回りすると元に戻ることになりますが、高熱源を冷やしたり、低熱源に熱を与えたりして周囲の環境のエントロピーを増大させているのです。

熱力学とエントロピー
物理の世界

カルノーサイクルと熱力学のポイント

熱力学はどうも人気が無いらしい。非常にとっつきにくく分かりにくい。私自身も大学での教養課程では、何だかエントロピーなんてあったなあ程度の記憶しかありません。退職後に色々読み直して、漸く分かりかけた段階です。
熱とか仕事とか、力学と比べかなり抽象的。更に偏微分∂なんか出て来る。ところで、ネットでカルノーサイクルが良く分からないとの質問がありました。質問者は、カルノーサイクルを扱う時に、大気圧をどう取り入れるのがということでした。カルノーサイクルの説明では、シリンダー内の理想気体の圧力は、p₀→p₁→p₂→p₃→p₀と変化するのですが、シリンダーの反対側の大気圧(p₀としますか)は、効率の計算には全く影響していません。ここで、熱力学の重要な法則；熱力学の第一法則を忘れてはいけません。熱力学の第一法則は、閉じた系を対象にしています。そして、ここで閉じた系とはシリンダーの内部だけです。高温熱源、低温熱源も外部の条件。ここで、系はサイクル運動を行ってます。1周回ると元の位置に戻るのです。つまり、大気圧はシリンダーに対して何も仕事をしていません。
熱力学の第一法則というのも、案外分かりにくい所があります。閉じた系に対して、熱と仕事がでたり入ったりします。系の中でエネルギーが保存されるのでなく、エネルギーが新たに突然、発生したり消滅したりしないということです。これは、ちょうど会社の簿記のようなもの。現金(熱)や商品(仕事)が出たり入ったり、金額ベースでは保存則が成り立っているようなものです。
理想気体の状態は、状態方程式f(p,V,T)＝0で表されます。たった3つの変数で表されるなんて大変便利なことです。p軸、V軸、T軸を取って、このfを表すと、3次元の曲面になってしまいますね。2次元なら普通の微分(接線方向)で間に合いますが、3次元の曲面では2方向の接線が必要。そのため、3つの変数のうちの一つを決めて(固定して)2つの接線方向を求めるのです。これが偏微分が頻繁に出て来る理由。その結果、各々の微分は全微分表示となります。
たとえば、dT＝∂T/∂V・dV＋∂T/∂p・dp
これは、温度の微小変化は、温度の体積に関する微小変化と圧力に関する微小変化の和として表されることを示します。温度と体積はバラバラには動けないわけ。
一方、△E＝△Q＋△Wでは、QとWを関係づけるものは何もないので、△をdと出来ないわけです。ｄは全微分可能な時だけに使える約束だからです。でも、Eについては、dEが使えるので、QとＷに´の付いた妙な記号が用いられています。熱力学独特な記号なので初めて見ると？？？となりますね。

カルノー以外のサイクル

カルノーサイクルは等温変化と断熱変化の組合せですが、それ以外にも色々なサイクルが考えられます。例えば、
      ①等圧・等積サイクル
      ②等圧・等温サイクル
      ③等温・等積サイクル
      ④断熱・等積サイクル
④は、オットー・サイクルとして知られているものでガソリン・エンジンの働きに近いとされています。①から④はどれも可逆過程となりますが、実際のエンジンで色々なロスがあり不可逆となるため効率がロスします。
【等圧・等積の場合】
このサイクルを下図に示します。

p-V図では、サイクルは長方形になるのでカルノー・サイクルよりもずっと簡単そうです。計算して見ると分かりますがこのサイクルで得られる仕事は当然、W＝(p₂－p₁)(V₂－V₁)で長方形の面積です。
p-V図では、等温線は直角双曲線のなるので、A、B、C、Dでの温度は異なることになります。温度が一番高いのがBで、一番低いのがDです。
簡単のため、シリンダー内の気体を1モルとすると、気体の状態方程式pV＝RTが成り立つので、各点での温度は次の通りです。
T_A＝p₂V₁/R、T_B＝p₂V₂/R、T_C＝p₁V₂/R、T_D＝p₁V₁/R、
そこで、このサイクルの効率を求めると
①A→B
W_A→B＝p₂(V₂－V₁)＞0(仕事をする)
Q A→B＝Cp(TB－TA)＝(Cp/R)( V2－V1) p2＞0(熱をもらう)
②B→C
W_B→C＝0(体積が変わらない)
Q _B→C＝C_V(T_C－T_B)＝(C_V/R)( p₁－p₂) V₂＜0
③C→D
W_C→D＝p₁(V₁－V₂)＜0
Q _C→D＝C_p(T_D－T_C)＝(C_p/R)( V₁－V₂) p₁＜0
④D→A
W_D→A＝0(体積が変わらない)
Q _D→A＝C_V(T_A－T_D)＝(C_V/R)( p₂－p₁) V₁＞0(熱をもらう)
結局、全体の仕事は、A→Bと C→Dの和で、
W＝p₂(V₂－V₁)＋ p₁(V₁－V₂)＝(p₂－p₁)(V₂－V₁)となり、長方形の面積です。
一方、もらった熱量は、D→A→Bの部分で、
Q₂＝(C_p/R)( V₂－V₁) p₂　＋(C_V/R)( p₂－p₁) V₁
となるけれども、効率ηは、 η＝W/ Q₂＝(p₂－p₁)(V₂－V₁)/{ p₂(V₂－V₁)＋(C_V/R)( p₂ V₂－p₁ V₁)}
となり、残念ながらカルノーのようにη＝1－(T₁/T₂)のように温度だけの綺麗な関係を得ることは出来ない。

熱力学とエントロピー
物理の世界
scienceの部屋

量子力学の世界

シュレディンガーの方程式

　シュレジンガー(Erwin Rudolf Josef Alexander Schrodinger)の方程式は、量子に関する工学的応用においては基本中の基本。ところが何故こうなるかと問われると、結局量子の世界はこういうものと理解するしかない。ここでは、簡単な誘導があったので紹介したい。ここで行うことは、ド・ブロイの波を一つの関数として、式を導くことです。まず、前提条件として
                E=hν    　　　　(1)
                p＝h／λ 　    　　　(2)
                E＝p^２／2m＋V    　　　(3)
ここで、(1)は、プランクのエネルギーの量子化、アインシュタインの光量子仮説で有名な式。νは振動数。h はプランク定数。 因みに ħ＝h/2πも良く使われる。二つ目の式(2)は、ド・ブロイの物質も波だという式。λはその波長。三番目の式は、普通のニュートン力学の力学的エネルギーです。p＝mvなので、第一項は(1/2)mv²と同じこと。Vはポテンシャルエネルギーです。波なので、
        ψ＝A exp{2πi(x/λ－νｔ)}　    　　(4)
これに、(1)、(2)を代入してλとνをEとｐで置き換えると、
        ψ＝A exp{2πi(px/h－Et/h)}　　　(5)
この(5)式をｘとｔで偏微分します。
        ∂ψ/∂x＝(2πip/h)ψ
        ∂ψ/∂t＝(－2πiE/h)ψ
この2式をħ＝h/2πを使って書き直して、
        －iħ∂ψ/∂x＝pψ　　(7)
        iħ∂ψ/∂t＝Eψ　　　(8)
また、(3)の両辺にψを作用させて、
        Eψ＝（p²/2m）ψ＋Vψ　　(9)
(9)式のEに(8)式を代入すると
        iħ∂ψ/∂t＝（p²/2m）ψ＋Vψ 　(10)
ところで、
        ∂2ψ/∂ｘ2＝(∂/∂ｘ)( ∂ψ/∂x)＝(∂/∂ｘ)(pψ/i ħ)＝(－p/ i ħ) ∂ψ/∂ｘ＝(－p/ iħ)²ψ＝－(p2/ħ²)ψ
すなわち、p²ψ＝－ħ²∂²ψ/∂ｘ²だから、(10)式は、
        iħ∂ψ/∂t＝（－ħ²/2m）ψ＋Vψ　　　(11)
これが求めるシュレジンガーの式です。
        iħ∂ψ/∂t＝－ ħ²/2m・ψ＋Vψ　　　(11)
ħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħħ

12歳の少年が書いた 量子力学の教科書

すごい本が出たものです。「入門書は易し過ぎ、専門書は難し過ぎ」ということを感じ、その間を埋める、入門書と専門書の架け橋になるような本があればいい…という想いを実現したのが本書だそう。数式を追いながら読めば理解が深まるのはもちろんですが、入門者の方がそこを飛ばして読んだとしても、「量子力学」に一歩迫ることのできる一冊です。 シュレディンガーやハイゼンベルグの考えも丁寧にハショラズに説明できる力は本物です。
　将棋では、藤井聡太四段の快進撃がニュースになりましたが、スポーツの世界を含めてどんどん若い世代が活躍していくことは楽しみですね。学校の勉強だけでは時代について行けなくなって来ているようですね。従来の教育や学習のあり方を抜本的に考える時期に来ているように思います。このことは我々定年後の勉強にも当てはまると思います。
        『12歳の少年が書いた量子力学の教科書』-近藤龍一；ベレ出版

scienceの部屋
物理の部屋

数学の部屋

目次 　　　

幾何学再入門	正四面体の重心と頂点のなす角度	ベクトル解析入門	部分積分と置換積分

幾何学再入門

　幾何学と言えば、総ての学問の基礎というのが欧米での常識。我が国では最近あまり人気がない。化学のおける立体構造や鉱物の結晶学等、空間図形は結構ややこしい。本当はユークリッド幾何の初歩からやればよいのでしょうが、それはそのうちにKids Roomの方で展開したいと思ってます。

正四面体の重心と頂点のなす角度

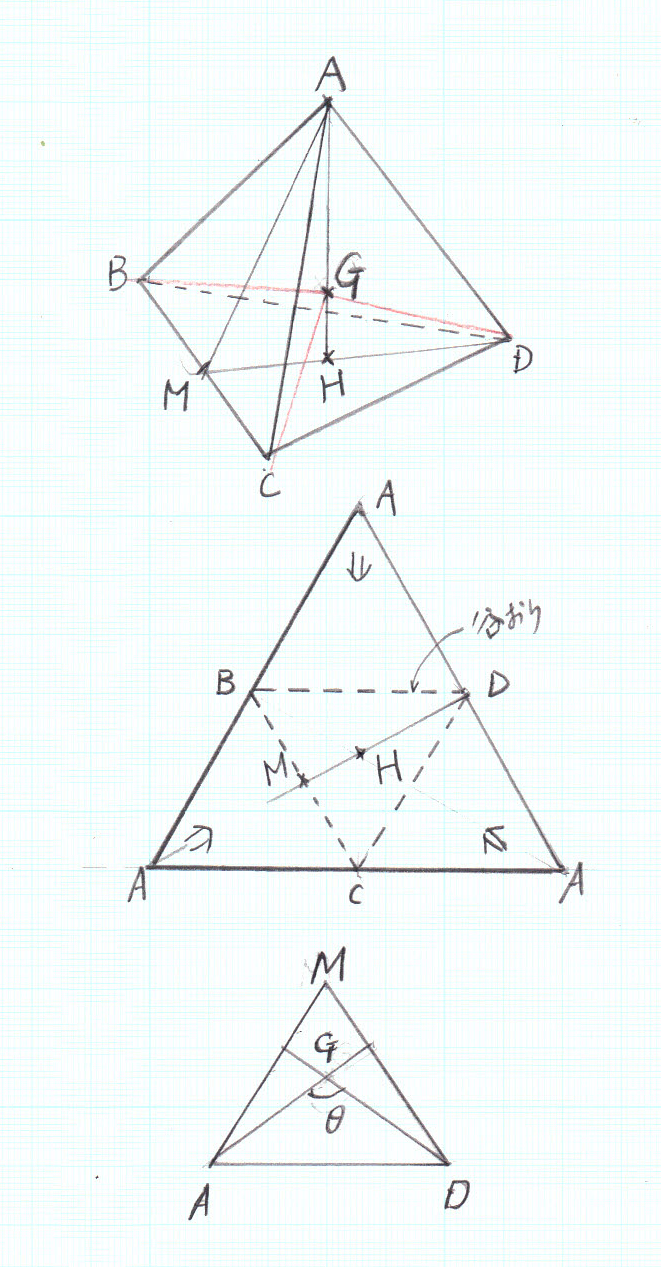　メタンCH₄の立体構造は、真ん中に炭素、正四面体の4つの頂点に水素分子が結合。H―C―Hのなす角度は109.5度となっています。この角度は正四面体の基本的な性質で、化学の問題でなく、自分で計算できる必要があります(化学の教科書には書いていない)。この計算は高１レベルでしょうが、立体図形でもあり結構考えにくいと思います。
　まず、正四面体の重心をG、４つの頂点をA、B、C、Dとします。図を参考にしてください。下図は上の立体の展開図です。正三角形が４つ集まっています。3つのAが折り返しで一つになります。正三角形の一辺をaとします。

さて、BCの中点をMとします。
AM＝DM＝(√3/2)a
Hを△BCDの重心とすると、DH＝(2/3)DM＝(2/3)×(√3/2)a＝(√3/3)a
AH＝√(AD²－DH²)a＝√(１－(√3/3)²)a＝√6/3a
ここで、重心Gは、AH上にあって、錐体(四面体)の重心であるから、AG：AH＝3:4
よって、AG＝(3/4)AH＝3/4×√6/3a＝√6/4a＝0.6123a=(1/1.633)a
ここで、△MADを考えると、AG＝DG
求めたい角度∠AGD＝θとして、余弦定理を適用する。
2AG・DGcosθ＝AG²＋DG²－AD²
2×(√6/4)a×(√6/4)a cosθ＝(√6/4)²a²＋(√6/4)²a²－a²
   ∴cosθ＝－1/3
ここからは、関数電卓の出番で、cos-1θ＝arccosθ＝1.9106 rad=109.47°として求めることが出来る。
ここで、錐体の重心位置および体積の求め方をレビューする。

錐体(底面積S)と三角形(底辺ｂ)の比較をしてみると良く似た関係がある。

図形	体積	重心位置
錐体	(1/3)Sh	(3/4)h
三角形	(1/2)bh	(2/3)h

錐体(底面積S)と三角形(底辺ｂ)の比較をしてみると良く似た関係がある。

数学の部屋 scienceの部屋