高校生にも分かる相対性理論
20世紀の物理学の2大成果としては、相対性理論と量子理論が挙げられるでしょう。量子論の方は大勢物理学の大家が成果を少しずつ積上げて行ったものですが、相対性理論の方は、天才アインシュタインがほとんど一人で作り上げていった感じのものです。相対性理論は、最初に完成された特殊相対性理論とそれから十年あまりの努力の結果生まれた一般相対性理論で構成されています。後者は、法則を記述するための新しい数学理論が必要だったので、数学嫌いの彼が、著名な数学者の助けを借りて猛勉強して、十年近くかけやっと完成したものだそうです。一生の間これほど勉強したことは無かったと本人も振り返っているそうです。真理を知ろうとする強烈なワクワク感があったのでしょう。
さて、最初の特殊相対性理論の方は、そんなに難しくありません。他の物理学者達も一歩手前までは達成していたようです。発想の転換が革命的だったのですね。それまでは、宇宙は、絶対静止した空間に単一の時間と言ったものがあるという前提がありました。でも、そのような前提では、光速が不変であることと、電磁波のマクスウェルの方程式が座標変換で不変にならないことを説明しきれないことから、時空(時間と空間の組合せ)が相対的にしか決められないことに気がついたそうです。
筆者も100年近く前に出来たこの理論を理解しようと取組んでみました。
| まずはローレンツ変換の式を理解する | ミンコフスキーの時空…準備 | ミンコフスキーの時空 | 横座標に関する疑問 |
| 原点の重ね合わせは必要ですか | 時空図での距離 | 縮む棒の長さ | 運動する時計は遅れる |
| 速度の足し算 | 運動する時計は遅れる | 運動による質量変化 | 質量とエネルギー |
まずはローレンツ変換の式を理解する
まず、ある観測者AとAに対して等速直線運動している別の観測者Bという物体があるとしましょう。空間ですからAの座標は(x,y,z)と3つの値が必要ですが、A～Bの運動の向きだけを考えれば、x一つだけで十分です。また、Bの座標(X,Y,Z)もXだけで十分です。つまり1次元の問題となります。また、宇宙空間を考えると、AとBの運動は相対的でどちらが動いているのか、判断は出来ませんね。
今、時刻t＝0、T＝0で、座標xとXの原点が0で一致するようにします(このように座標を決めます)。そこで、光がx方向(または、X方向)に発射されたとします。
話を分かりやすくするためにもう少し具体的なイメージを考えます。いわゆる思考実験。2人の観測者AさんとBさんはあなたのお友達で、互いに速度差vを持って動いています。そこであなたが光だったとします。光速の乗り物でも構いません。あなたはAさんからも、Bさんからも同じ光速（c）で遠ざかっています。光速が不変であることは、今まで物理学で実測して何度も確かめれた事実です。
今までの普通の考えでは、Aに固定した座標系(x,t)ではBの座標は、X＝x－vt と表されます。Aの位座標は、逆にBの座標(X,T)では、x＝X＋vTとなります。
Aの座標で光の速さをcとすると、Bは、光と同じ方向に進んでいるので、Bの座標では光速はc－v、また、Bの座標で光速をcとすると、Aは、Bと反対方向に進んでいるのでAの座標では、光速はc＋vになるはずです。ところが、光の速度を実験で確かめると、どちらの座標でも光速は常にcであることが確認されました（マイケルソン・モーリーの実験など）。これ当時の物理学の世界では大変なことだったんですね。なんでやねん！そこで、宇宙全体は絶対静止しており、唯一の時間があるとの考えを捨てれば、光速を一定にするようなAとBとの間の座標の変換法則を探せば良いことが分かります。でも、実際にはこの考え方を捨てるにはかなりの勇気が必要だったようです。
Aの座標を(t,x)、Bの座標を(T, X)とします。ここで注意して頂きたいのは、この座標系は私たちが今まで慣れているものと異なり、時間と位置の組合せになっていることです。このような組合せを時空と呼んでいます。だから、一次元の直線状の運動を考えているはずなのに、二次元時空(1次元の時間と1次元の位置)で考えていることになるのです。われわれの暮らしている実際の世界も3次元空間ですが、時間を考慮すれば4次元時空ということに。決して4次元空間ではありません。
変換法則は互いに対称で相対的なので以下のような一次式で表わされるでしょう。 γ は光速を不変にするための係数です。空間の相対性(AとBは立場対等ということ)から、(1)、(2)の変換、逆変換の係数は同じ γ を使うのが妥当でしょう。(3)式と(4)式はあなた（光の先端）の位置を両方の座標で示したものです。
*赤字で示した"γ"はギリシャ文字でガンマと言う字です。Webでの表示をみると英語の"Y"見たいですが。
今までの、議論をまとめると、求めたい座標変換は次の4つの式を満足します。未知数は、x、X，t、Tの4つと求めたい γ の5つですが、定数項が無いのでγは簡単に求まります。
X＝γ(x－vt) (1)
x＝γ(X＋vT) (2)
x＝ct (3)
X＝cT (4)
(3)(4)を(1)(2)に代入すると、x、Xが消去された式が得られます。
cT＝γ(c－v)t (5)
ct＝γ(c＋v)T (6)
この(5)、(6)式の両辺を互いに掛け算して見ましょう。こうすれば、tとTが同時に消えて、 γ の正体が分かります。
すなわち、 c2 T t＝γ2 (c－v)(c＋v) t T、 両辺から時間tとTが消せます。ここまで来れば計算は簡単でしょう。
γ2＝c2 / (c2－v2)
γ＝c / √(c2－v2)＝1 / √(1－β2)… (6)、ただし、β＝v / c …(7)
やっと、時空座標の変換式が求まりました。html文書で作った数式は見にくいので、手書きのものを上図にまとめています。
沢山の入門書ではもこれをもとに色々な時空のパラドックスを説明されています。大勢の人達がアインシュタインの時空の相対性の考え否定しようとして色々なパラドックス考えて来ました。一々相手していると頭がこんがらかって来るでしょう。
でも、アインシュタインはニュートン等によってつくられて来た世界を完全に否定しているわけではないことに注意して下さい。
対象としている速度ｖが光速cに比べて小さい時はβ≒0なので、γ≒1となり、これはガリレオ変換と言われる我々が今まで使っているものと全く同じもの。つまり、人類の科学技術が進歩して光りに比べて無視できない大きさの速度を考えないといけなくなったと言うことです。
つまり、特殊相対性理論は、ニュートン力学を包含するより大きな理論の枠組みを作ろうとする試みでもあったわけです。だから、この枠組みを完成するためには更に進めて一般相対瀬理論まで挑戦しないといけなかったわけです。特殊と言う意味は加速度のない等速直線運動という極めて特殊な状態しか取り扱えないからです。
少し、補足を。今１次元だけの運動を考えています。観測者AとBは各々光が発せられたことを確認します。AとBの各々の時空が(x,t)、(X,T)で、光りが発せられた事象の時空を各々(0,0)、(0,0)と設定します。AとBは異なった速度で等速運動しています。相対速度としてBはAに対してvの速度で動いています。γ＝1ならば、普通我々が考えている座標の変換です。でも、それでは光速に差が出てくるはず。でも、光速はどちらの時空でも一定(c)です。つまり、あなたが光とすると、あなたの位置は(3)、(4)式の通りでしょう。そして、あなたの位置は(1)、(2)の変換式で互いに交換可能なはずです。そう考えると γ は自然と決まります。
このγは、ローレンツと言う科学者が、光にはエーテルと言う媒質があると仮定して導いたものと同じ形なのでローレンツ変換と呼ばれています。
ミンコフスキーの時空…準備
前節では、2つの点A，Bに各々とった時空座標の間の座標の変換式を考えました。AとBとは互いに等速運動をしており、BはAからｖの速度で遠ざかっています。AとBとの座標軸は同じ向きでした。ここでは、ちょと一工夫して、時間については光速cをかけたものを座標と考えましょう。そうすると、ctは距離の単位となり、後でグラフを描く時に便利です。でもこれは凄ーく壮大な世界ですね。1ctとは光が1秒間に進む距離ですから。
A、Bの時空座標をそれぞれ、(x, ct)、(X, cT)とすると、
A,B間の座標変換は一般には、次の形で表されます。
X＝F(x, ct),
T＝G(x, ct)
また、逆変換は、
x＝f(X, cT)
ｔ＝g(X, cT)
特殊相対性の理論では、この関数F、G、f、gは簡単な一次式で済みますが、一般相対性理論では、この関数の形を決めることが大きな課題となるのでしょう。前節では、F，fの形は次のように求めました。
X＝γ(x－βct)> (1)
x＝γ(X＋βcT) (2)
ただし、β＝v/c でβは光を基準にした速度です。
ここから、(2)を(1)に代入して、ｔ＝g(X, cT)が、(1)を(2)に代入して、T＝G(x, ct)が求まります。すなわち、
cＴ＝γ(ｃｔ－βｘ) (3)
cｔ＝γ(ｃＴ＋βｘ) (4)
要するに(1)(3)の組が(x,t)→(X,T)とする変換、(2)(4)の組が(X,T)→(x,t)となる逆変換です。
見やすくするため、手書きの計算を示しました。最終結果は、マトリックス表示をすると非常にきれいな形になります。
行列で示すと、この行列がきれいな対称行列になっていることが分かる。ちなみに専門家達は、（ct,cT）の代りに変数を(τ，Τ)と考えて、これを改めて(t,T)と表示してしまうのだそうだ。出来るだけ表示を簡素に見やすくすることがややこしい式を分かりやすくするコツだ。
ミンコフスキーの時空
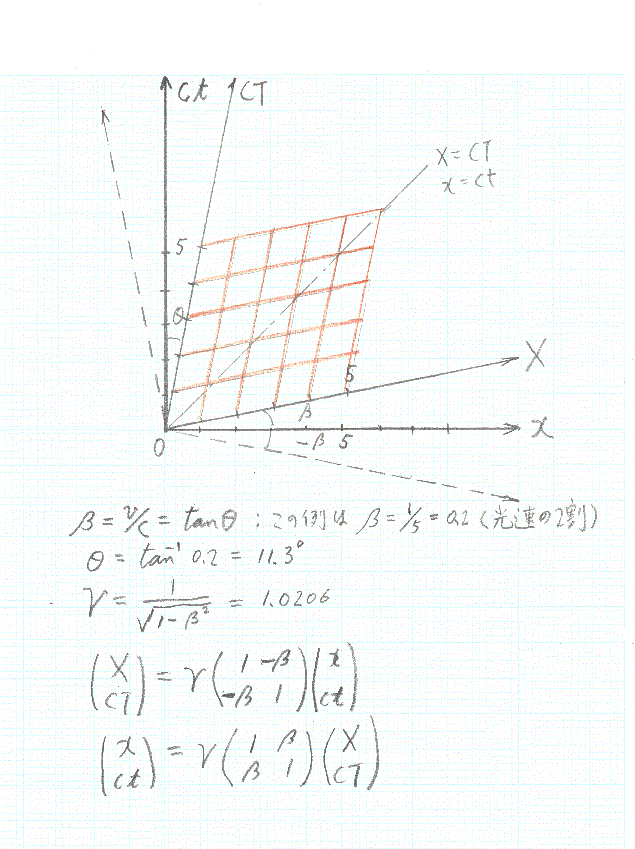
やっと出てきました。ミンコフスキーの時空図です。ミンコフスキーはアインシュタインの数学に恩師で、相対性理論の構築にも数学面でアインシュタインを大いに助けました。持つべきものは良い師ですね。ここで、座標(x,ct)、(X,cT)を同時に表示しようとすると、図のように斜交座標を用いることになります。
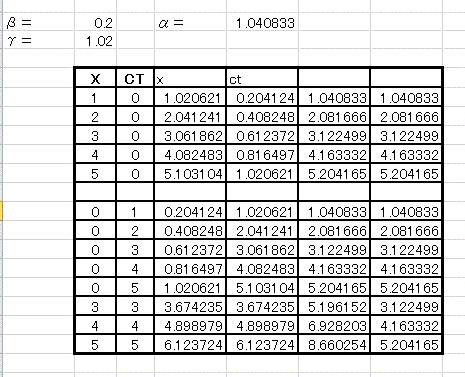
Ｘ軸の傾きは、tanθ＝β＝v/cになります。cT軸も同じに傾けます。座標(x,ct)と(X,cT)の変換は、前節で求めた(1)～(4)で簡単に求まります。添付の表では、X軸、CT軸に相当する(x,ct)座標を求めて、そこからX軸、cT軸のx、ctに対応する値を求めて見ました。一方、値は係数√（（1＋β2）/（1－β2））をかけても求まります。
ところで、この時空図で各座標軸の単位はどうなっているのでしょうか。例えば、x＝5とあれば、これは5mとしてもかまいません。その時のcT軸の5は、光が5m進むのに必要な時間を表します。また、これを5光年と読むと、cT軸の5は、光が5光年進む時間、つまり5年を表します。
さて、斜交座標のメシュは赤線で示したようになります。X軸はcT＝0を示しています。反対にcT軸はX＝0を示します。x軸もct＝0、ct軸もx＝0を示します。
ここで、今までのことをもう一度、整理してみるために、変換式と時空図をちょっとかきかえます。ctを単にｔで表します。その時間は光が進む距離です。速度はβの代わりに単にvと書くことにします。光に対する相対速度(v/c)です。すると、求めた変換式は、つぎのようにとても見やすい形に書き直せます。相対論の入門書では、色々な書き方をしていますが、この形が最もシンプルです。v→v/c、t→ctのように読み替えて行けば、簡単に元の形に戻せます。
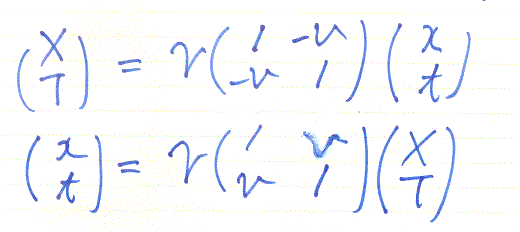X＝γ(x－vt) (1)
x＝γ(X＋VT) (2)
T＝γ(t－vx) (3)
t＝γ(T＋vX) (4)
γ＝1/√(1－v2) (5)
このように表記すれば、相対論では位置と時間が全く対等に取り扱われていることが良く分かります。
簡略化したマトリックスの式は右の通りです。ずいぶんスッキリしてきます。
横座標に関する疑問
空間は３次元ですから、運動に垂直の方向、ｙ、ｚ軸方向に対しては座標に変換はどうなるのでしょうか。横方向に対しても空間の等質性を仮定します。
Y=K(v)y、ｙ＝K(－v)Y とすると、K(v)K(－v)＝1、K(v)＝K(－v)のはずなので(等質性)、K2=1からK=1となります(－1は不適)。Z方向も同様にして、K＝１です。結局、横方向は簡単で Y=ｙ、Z=zとして問題ないことが分かります。
原点の重ね合わせは必要ですか
X-Tの原点座標がx-tの座標で（a, b）だとしますと、x＝tの代わりにx－a, t－bを新しくｘ-ｔ座標とすれば重ねることが可能です。原点をそろえることはそれほど無理な仮定ではないと思います。
時空図での距離
この時空図の上で、距離というものを定義します。
s2＝ct2－x2－ｙ2－z2
今は、空間はx方向だけを考えていますので、
s2＝(ct)2－x2 となります。
となります。ここからが普通のユークリッド幾何と異なります。距離sが0となるのは、x＝±ctですから、45度の直線上ですべて距離0です。
また、時空は下の図に示すような領域に分けることが出来ます。ここで定義した距離は、虚数の場合もあり、この領域を空間的領域と言います。また、xが実数の時は、時間的領域と言いますが、x軸より上の部分を「未来」、下の部分を「過去」とします。また、このミンコフスキーの空間では、普通の三角不等式AC＜AB＋BCは成立せず、逆にAC＞AB＋BC (相対論的三角不等式)となります。面白いですね。
縮む棒の長さ
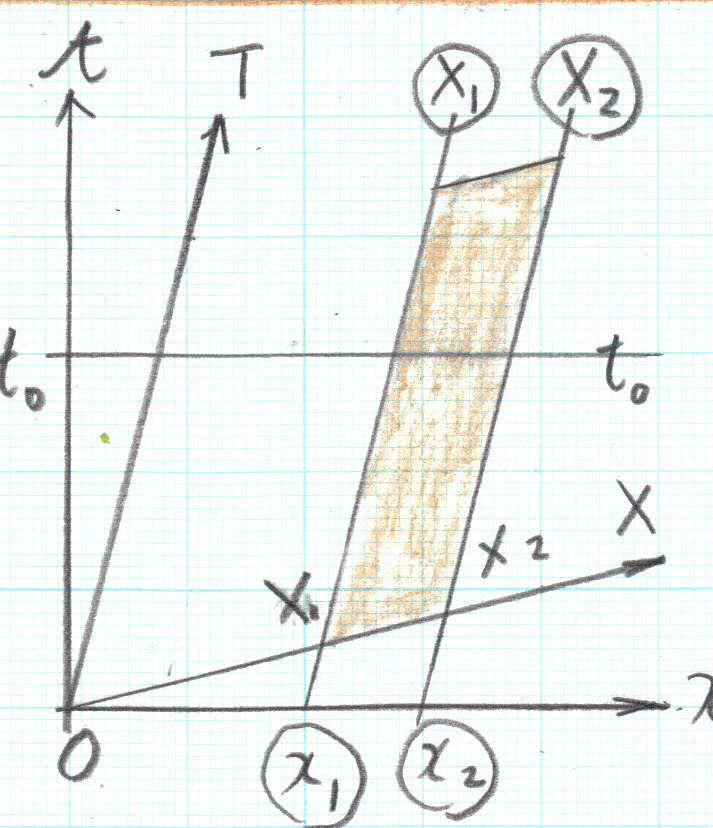X軸とともに動く棒(長さをL0とします)を考えます。L0を固有長と言います。もっと明確に言えばX軸の固定された棒ですね。棒の両端のX座標をX1、X2とすると、
L0＝X2－X1。棒は、T軸に平行に進み、X1、X2は移動中変化しません（X軸に固定されているので当然ですね）。これをx座標で観測すると、棒の両端に位置は、x座標におかれている時計で同じ時刻に計らねばなりません。従って対応する時刻をｔ1＝ｔ2＝ｔ0として、x軸での棒の長さをLとします。座標変換の式を用いて、
X1=γ(x１－vt1), X2=γ(x2－vt2)
従って、X2－X1=γ(x2－x1),
つまり、x2－x1＝L＝L0/γ,
γ＞1だから、L＜L0
このことをもって、動いている物は進行方向に縮むと言われているのです。しかし、実際問題として棒の両端を同時に計ることは大変難しいことです。光にも速さがあるので情報を伝達するまでにある程度の時間がかかってしまうからです。写真を撮れば光速で動く物体は縮んで写っているのでしょうか。そのようなことは無いことが分かっています。このような誤解から、縮む棒、遅れる時計(この後説明します)に関するいろいろなパラドックスが提案(相対論に懐疑的な論客から)されています。この辺、一般の入門書では、これでもかこれでもかとパラドックスを持ち出して解明していきます。説明者にとっては大変面白い話題で読者も楽しめると思ってのことでしょうが、たいていの読者はここでうんざりして、相対論を投げ出してしまう一因にもなっているようです。特殊相対論もまだまだ、興味のある話題は尽きません。まず、最初目標、かの有名な公式E=mc2を導く所までは進みましょう。
運動する時計は遅れる
X座標の固定された時計を考える。t＝0、T=0でx＝0、X=0とする。X軸は、x軸の正方向に速度vで動いている。x軸上(x＝0)で観測する、時計が時刻t1であったとします。
座標変換式から、 t1=γ(T1+ｖX)から。
t１=γT1、 すなわち T1=ｔ1/γ＜ｔ1。
運動している時計の時刻T1は、静止した時計の時刻ｔ1よりも遅れていると観察されることになる。なお、時計に対して静止している系で測られる時間を「固有時間」と呼ぶ。これも運動している時計を望遠鏡で見たり、写真を撮ったりすると遅れて見える訳ではないことに注意されたい。。
速度の足し算
x-ｔ座標系(Aさんの座標系としましょう)に対して、X-T座標系（こちらはBさんの座標系とします）は速度Vで移動しています。BさんのX-T座標系に対して、速度Uで移動している粒子を考えます。今までの考えでは、Bさんの座標系で動いている粒子は、Aさんの座標系ではv+Uとなってしまいます。もし、この粒子が光（光子）だったら、Aさんから見た粒子はU+cの速度になってしまいます。これは光速より速いことになり明らかに矛盾です。
けれども、ミンコフスキー空間（時空）で考えるとこの矛盾は容易に解決します。
ただし、ここでは速度V、Uは相対速度(V=v/c, U=u/c)としました。すると、この時の粒子のx座標に対す速度Wはどうなるでしょう。
まずは座標変換式を用いて、Bさんの座標系の粒子の時空をAさんのものに変換しましょう。Aさん、Bさんの座標の上での粒子の速度は、各々dx/dt、dX/dTとなることに注意して下さい。
x＝γ(X+VT) → dx＝γ(dX+VdT),
t＝γ(T+VX) → dt＝γ(dT+VdX) ですから、
Aさんの座標上での粒子の速度は次のようになるでしょう。
W＝dx/dt＝γ (dX+VdT)／γ (dT+VdX)＝（dX/dT+V）／(1+VdX/dT)＝(U+V)／(１+UV)
これを普通の速度に直すと、W＝w/c、U=u/c、V=v/cとして、
w＝(u+v)／(1+uv／c2)-----①
が求められます。
この①式はとても有名な式ですね。この式でu≦c、v≦cであればニュートン力学の普通の合成速度となります。また、u＝cとなっても、w＝cで光速を越えることがないことが分かります。
でも、この式は光よりも速い粒子が存在しないといっているわけではありません。ただ我々の知識では見つけることが出来ないだけかも知れません。でも、ここまでの議論を見てきた人はアインシュタインが突拍子もないアイデアを考え付いたのではないことが理解できると思います。互いに等速運動しているどんな座標系で観測しても光の速度は一定になるという事実を認めれば必然的にこのようになるということです。
運動による質量変化
(x,y,z)座標系にの原点に質量m0の弾性球が静止している。一方、この座標系に対して、速度vで運動している(X,Y,Z)座標系の原点にも同じ弾性球が静止している。x座標系の時刻tでこの弾性球同志が衝突(速度v)する。その結果、x座標系ではy方向に速度u、X座標系では、－Y方向に－uで動き出した。y＝Yであり、ここまではいいでしょう。X座標系での対応する時刻は(時刻の座標変換)、
T＝γ(t－x)
x方向には動いていないので、x＝0であり、T＝γt
つまり、x座標系から見るとX座標系における時間は係数γだけ間延びしており、x座標系において運動量の保存則が成立しているとすると、
m0u＝mu/γ
つまり、m=γm0となって、質量は運動によって変化(増加)する。
質量とエネルギー
質量が運動によって変わるので運動量は、
p＝γm0ｖ
力＝質量×加速度 は 力＝運動量の時間的変化と置き換えられる。
F＝dp/dt
この時、単位時間当たりの力がする仕事はF・vである。
運動エネルギーTは、エネルギーの時間的変化が単位時間にした仕事に等しいので、
dT/dt＝F・v
ここから、総エネルギーとして、
E＝ｍｃ2
となる。計算の詳細は、下記に示す。
agl;dgjd